CAIE IGCSE CS revision - Unit 1 (2023)

【点此返回复习要点目录】

如遇到公式加载异常，请刷新页面！

Unit 1 Data representation 数据表示

1.1 Number systems 数字系统

• 大纲要求

1.1.1 Understand how and why computers use binary to represent all forms of data 了解计算机如何以及为何使用二进制来表示所有形式的数据

• Any form of data needs to be converted to binary to be processed by a computer 任何形式的数据都需要转换成二进制才能被计算机处理
• Data is processed using logic gates and stored in registers 数据使用逻辑门处理并存储在寄存器中

• 现实生活中存在多种进制，但计算机仅能理解和使用二进制进行计算与问题处理。任何其他进制都需要先转换成二进制。
• 数据有指定的存储位置和计算方式，具体可参考之后的学习内容。

1.1.2 (a) Understand the denary, binary and hexadecimal number systems 了解二进制、二进制和十六进制数字系统

• Denary is a base 10 system 十进制是一个以10为基数的系统
• Binary is a base 2 system 二进制是以2为基数的系统
• Hexadecimal is a base 16 system 十六进制是以16为基数的系统

• Denary：十进制，数字逢十进一，每位是0~9中的某个数字。十进制是日常生活、普通数学等最常用的数字系统。
  • 比如：6，36，728等。
  • 为了区别于其他进制，十进制数字可用下角标10或D来区分，如(36)₁₀或(36)_D。
• Binary：二进制，数字逢二进一，每位是0~1中的某个数字。二进制是计算机唯一能理解的数字系统。
  • 比如：10，1001，1100010等。
  • 为了区别于其他进制，二进制数字可用下角标2或B来区分，如(1001)₂或(1001)_B。
• Hexadecimal：十六进制，数字逢十六进一，每位是0~9、A~F中的某个数字（或字母）。A代表十进制中的10，B代表11，以此类推。
  • 比如：7，F，31A等。
  • 为了区别于其他进制，十六进制数字可用下角标16或H来区分，如(31A)₁₆或(31A)_H。
• 各数字系统之间的数值对应（前16个数值）：

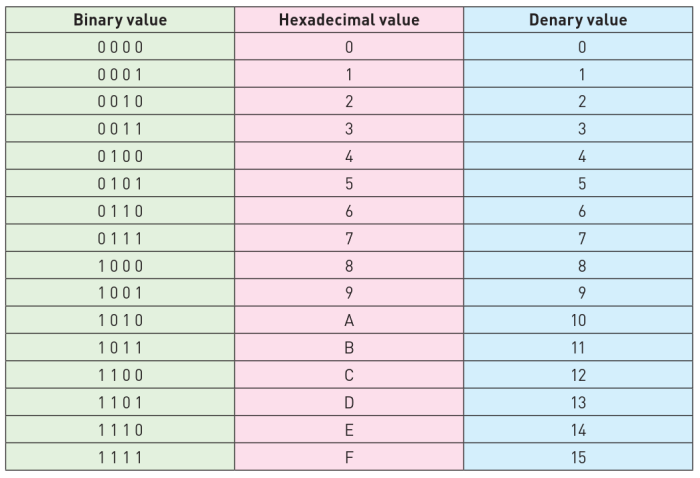
1.1.2 (b) Convert between (i) positive denary and positive binary (ii) positive denary and positive hexadecimal (iii) positive hexadecimal and positive binary 在(i) 正十进制和正二进制之间转换 (ii) 正十进制和正十六进制 (iii) 正十六进制和正二进制

• Values used will be integers only 使用的值将仅为整数
• Conversions in both directions, e.g. denary to binary or binary to denary 双向转换，例如十进制到二进制或二进制到十进制
• Maximum binary number length of 16-bit 最大二进制数长度为 16 位

• 十进制转二进制：
  • 方法1：不断减去不超过本数字的2的最大次方数（包括0次方），直到差为0。
    • e.g. 将十进制的142转换为二进制。则142-128=14（2⁷位标1）；14-8=6（2³位标1）；6-4=2（2²位标1）；2-2=0（2¹位标1）。其他数位标0。则转换后的数字为10001110。

27=128	26=64	25=32	24=16	23=8	22=4	21=2	20=1
1	0	0	0	1	1	1	0

（!!!!!!!!!!!表格）

• • 方法2：本数字不断除2，取余。当商为0时，余数倒置。
    • e.g. 将十进制的142转换为二进制。则142不断除2后取余数倒置，得到10001110，计算过程如下图所示。

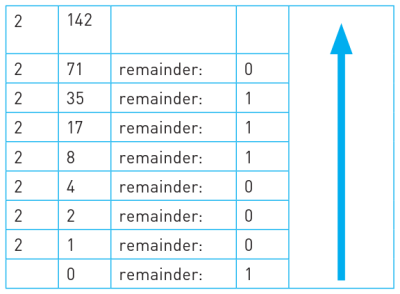
• 二进制转十进制：将二进制所在数位的2ⁿ与数位值相乘，然后将各乘积相加。
  • e.g. 将二进制的11101110转换为十进制。则有1×2⁷+1×2⁶+1×2⁵+0×2⁴+1×2³+1×2²+1×2¹+0×2⁰= 128+64+32+8+4+2 = 238。

• 十进制转十六进制：本数字不断除16，取余。当商为0时，余数倒置。
  • e.g. 将十六进制的2004转换为十进制。则2004不断除16后取余数倒置，得到7D4（10~15的余数需要换成对应字母），计算过程如下图所示。

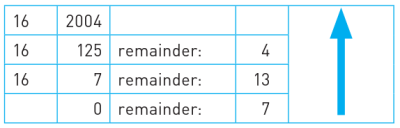
• 十六进制转十进制：将十六进制所在数位的

与数位值相乘，然后将各乘积相加。

• • e.g. 将十六进制的45A转换为十进制。则有4×16²+5×16¹+10×16⁰= 4×256+5×16+10×1 = 1114。

• 二进制转十六进制：从二进制数末位起，从右往左每四位一组（位数不够用0补齐）。然后将每个四位二进制数换为十六进制数，连接在一起。
  • e.g. 将二进制数10000111111101转换为十六进制。则先将二进制数拆分为4个数位一组，有0010 0001 1111 1101，然后每一组写成一个十六进制数，得到21FD。

• 十六进制转二进制：将每个十六进制数位写成4位的二进制数（位数不够用0补齐）。然后将每个二进制数连接在一起。
  • e.g. 将十六进制数45A转换为二进制。则将45A的每个数位换成4位二进制，得到0100、0101和1010，然后将它们连接起来，得到转换后的二进制数010001011010。

1.1.3 Understand how and why hexadecimal is used as a beneficial method of data representation 了解十六进制如何以及为何被用作一种优秀的数据表示方法

• Areas within computer science that hexadecimal is used should be identified 应确定使用十六进制的计算机科学领域
• Hexadecimal is easier for humans to understand than binary, as it is a shorter representation of the binary 十六进制比二进制更易于人类理解，因为它是二进制的更短表示形式

• 十六进制在计算机中的常用领域包括：
  • Error codes 错误码
  • MAC addresses MAC地址
  • IPv6 addresses IPv6地址
  • HTML colour codes HTML颜色码

1.1.4 (a) Add two positive 8-bit binary integers 将两个正8位二进制整数相加

• 二进制加法：按照“逢二进一”的原则，挨个数位相加即可。
  • 注意：可能出现溢出，具体解释【参考1.1.4(b)】。
  • e.g. 00100111 + 01001010的计算过程如下图所示：

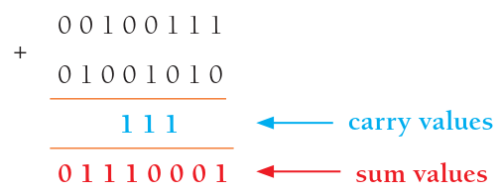
1.1.4 (b) Understand the concept of overflow and why it occurs in binary addition 理解溢出的概念以及为什么它会出现在二进制加法中

• An overflow error will occur if the value is greater than 255 in an 8-bit register 如果8位寄存器中的值大于255，则会发生溢出错误
• A computer or a device has a predefined limit that it can represent or store, for example 16-bit 计算机或设备具有可以表示或存储的预定义限制，例如16位限制
• An overflow error occurs when a value outside this limit should be returned 当应返回超出此限制的值时会发生溢出错误

• Overflow：溢出，指数字超过了存储数位限制的情况。当出现溢出问题时，计算机或者返回错误信息，或者忽略溢出数位（这会导致该数字不准确）。
  • e.g. 当计算正二进制的加法01101110 + 11011110时，得到的结果为101001100，数位为9位，超过了原寄存器8位的数位限制，发生溢出。
  • 可能的解决方法：可考虑修改规则或者更换硬件来扩大数位限制，如将8位限制提高至16位限制。

1.1.5 Perform a logical binary shift on a positive 8-bit binary integer and understand the effect this has on the positive binary integer 对一个正8位二进制整数执行逻辑二进制移位并理解这对正二进制整数的影响

• Perform logical left shifts 执行逻辑左移
• Perform logical right shifts 执行逻辑右移
• Perform multiple shifts 执行多次移动
• Bits shifted from the end of the register are lost and zeros are shifted in at the opposite end of the register 从寄存器末尾移出的位丢失，零移入寄存器的另一端
• The positive binary integer is multiplied or divided according to the shift performed 正二进制整数根据执行的移位进行乘法或除法
• The most significant bit(s) or least significant bit(s) are lost 最高有效位或最低有效位丢失

• Logical left shift：逻辑左移，相当于二进制数值乘2。
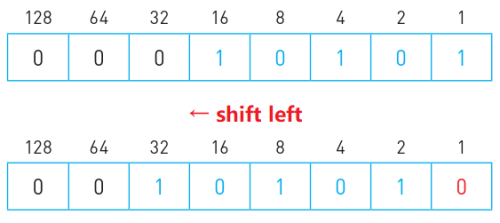
  • 操作方法：所有数位向左移一位（如果此前已满最高数位，则最高位溢出，抹去），末位以0填充。
  • e.g. 将10101执行逻辑左移，如图所示。

• Logical right shift：逻辑右移，相当于二进制数值除2。
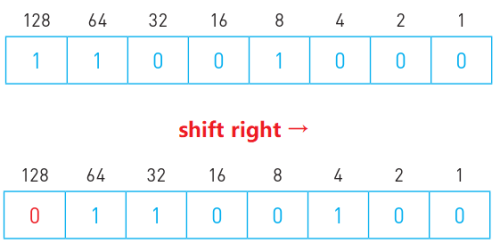
  • 操作方法：所有数位向右移一位（最低位溢出，抹去），首位以0填充。
  • e.g. 将11001000执行逻辑右移，如图所示。

1.1.6 Use two’s complement to represent positive and negative 8-bit binary integers 用二进制补码表示正负8位二进制整数

• Convert a positive binary or denary integer to a two’s complement 8-bit integer and vice versa 将正二进制或二进制正整数转换为二进制补码 8 位整数，反之亦然
• Convert a negative binary or denary integer to a two’s complement 8-bit integer and vice versa 将负二进制或二进制整数转换为二进制补码 8 位整数，反之亦然

• Two’s complement：补码，指二进制数值的补数。
  • 正数的补码是其本身，无需进行计算。
  • 负数的补码计算方法如下：
    • 方法1：按照定义进行计算。先按照负数的绝对值（十进制）写出对应的二进制数（8位，位数不满以0补齐），然后每位取反，最后加1。
• e.g. 写出-67的补码。则先写出绝对值67的二进制数01000011，然后每位取反得到10111100，然后再加1，得到补码为10111101。
  • • 方法2：先按照负数的绝对值（十进制）写出对应的二进制数（8位，位数不满以0补齐），然后从末位开始，忽略掉所有0和第一个不为0的数位，然后对未忽略的数位每位取反，然后和忽略掉的数位连接。
• e.g. 写出-67的补码。则先写出绝对值67的二进制数01000011，然后忽略掉末位开始的所有0和第一个不为0的数位（即最后一位的1），之前的数位全部取反（对0100001这些数位取反，得到1011110），然后将忽略掉的数位连接到取反的数位后面，得到补码为10111101。

1.2 Text, sound and images 文字、声音和图像

• 大纲要求

1.2.1 Understand how and why a computer represents text and the use of character sets, including American standard code for information interchange (ASCII) and Unicode 了解计算机如何以及为何表示文本以及使用字符集，包括美国信息交换标准代码 (ASCII) 和 Unicode

• Text is converted to binary to be processed by a computer 文本被转换为二进制以供计算机处理
• Unicode allows for a greater range of characters and symbols than ASCII, including different languages and emojis Unicode允许使用比 ASCII 更大范围的字符和符号，包括不同的语言和表情符号
• Unicode requires more bits per character than ASCII 与 ASCII 相比，Unicode 每个字符需要更多的位数

• 计算机需要将文字转换成二进制数值才能进行理解和处理。将人类的自然语言转换为二进制数值需要用到字符集中的对应规则。

• ASCII code：指美国信息交换标准代码，由7位二进制数字组成，包括了常见的一些字符，共128个（十进制序号为0~127）。常用序号如下（以十进制表示）：
  • No.32: <space>（空格）
  • No.48~57: 0~9
  • No.65~90: A~Z
  • No.97~122: a~z

• Unicode：指统一码（也称万国码），试图囊括所有语言的所有字符。常见的Unicode有UTF-8、UTF-16等。因为包括的字符数量庞大，因此每个字符的表示比ASCII码需要更多的二进制位数。
  • 注意：Unicode具体的表示规则不在考纲范围内，可在A-Level阶段继续学习。

1.2.2 Understand how and why a computer represents sound, including the effects of the sample rate and sample resolution 了解计算机如何以及为何表现声音，包括采样率和采样分辨率的影响

• A sound wave is sampled for sound to be converted to binary, which is processed by a computer 对声波进行采样，将声音转换为二进制，由计算机处理
• The sample rate is the number of samples taken in a second 采样率是一秒钟内采集的样本数
• The sample resolution is the number of bits per sample 样本分辨率是每个样本的位数
• The accuracy of the recording and the file size increases as the sample rate and resolution increase 文件记录的准确性和文件大小随着采样率和分辨率的增加而增加

• Sound：声音。
  • 声音的三大要素：frequency频率、wavelength波长和amplitude振幅。
  • 注意：自然界中的声音被称为analogue data模拟数据，无法被计算机直接处理，需要通过analogue to digital converter (ADC)模拟-数字转换器来转换成digital data数字数据（即二进制数值），才能被计算机理解和处理。

• Sampling：指采样操作。从analogue data模拟数据转换成digital data数字数据的过程中，需要进行sampling采样操作。采样操作中的重要指标包括：
  • Sampling resolution (bit depth)：采样分辨率（位深），采用多少位的二进制数字来表示采样的结果数值。
  • Sampling rate (Hz)：采样率，指每秒从模拟数据中的采样数量。比如44100Hz指每秒采样44100次（满足人耳听觉连贯性的采样率至少需要40000Hz）。
  • Time intervals：时间间隔，指采样时间的间隔，是采样率的倒数。
  • 注意：声音文件的准确性（对模拟数据的还原度）随着采样率和采样分辨率的提高而提高，但文件大小也随之增加。

1.2.3 Understand how and why a computer represents an image, including the effects of the resolution and colour depth 了解计算机如何以及为何表示图像，包括分辨率和色深的影响

• An image is a series of pixels that are converted to binary, which is processed by a computer 图像是一系列转换为二进制的像素，由计算机处理
• The resolution is the number of pixels in the image 分辨率是图像中的像素数
• The colour depth is the number of bits used to represent each colour 颜色深度是用于表示每种颜色的位数
• The file size and quality of the image increases as the resolution and colour depth increase 图像的文件大小和质量随着分辨率和颜色深度的增加而增加

• Bitmap：位图。计算机通常使用位图来表示图像。位图中的重要指标包括：
  • Pixels：像素，指位图的最小组成单位，有固定的位置和颜色。
  • Colour depth：色深，指采用多少位的二进制数字来表示一种颜色。常见的色深包括8-bit、10-bit等。
    • 注意：如果采用8-bit的色深，则红绿蓝三基色均有2⁸=256种二进制数值，因此每个像素点可供选择的颜色有256×256×256=16777216种。
  • Image resolution：图像分辨率，指每英寸图像内有多少个像素点（单位为dpi），以长×宽的形式表示，比如1024x768。
  • 注意：图像文件的质量（清晰度、色彩还原程度等）随着色深和图像分辨率的提高而提高，但文件大小也随之增加。
  • Pixelated：像素化，指图像模糊，可以看到像素点的情况。

1.3 Data storage and compression 数据存储与压缩

• 大纲要求

1.3.1 Understand how data storage is measured 了解如何衡量数据存储

• Including: 包括：
- bit比特
- nibble半字节
- byte字节
- kibibyte (KiB) 千比字节 (KiB)
- mebibyte (MiB) 兆比字节 (MiB)
- gibibyte (GiB) 吉比字节 (GiB)
- tebibyte (TiB) 太比字节 (TiB)
- pebibyte (PiB) 拍比字节 (PiB)
- exbibyte (EiB) 艾比字节 (EiB)
• The amount of the previous denomination present in the data storage size, e.g.: 数据存储大小中，与存在的先前单位的换算，例如：
- 8 bits in a byte 1字节等于8比特
- 1024 mebibytes in a gibibyte 1吉比字节等于1024兆比字节

• Bit：比特，指二进制数值中的1个位数，是计算信息量中的最小单位。
• Nibble：半字节。1 nibble = 4 bits
• Byte：字节。1 byte = 8 bits
• Kibibyte (KiB)：千比字节。1 KiB = 2¹⁰ bytes = 1024 bytes。
• Mebibyte (MiB)：兆比字节。1 MiB = 2²⁰ bytes。
• Gibibyte (GiB)：吉比字节。1 GiB = 2³⁰ bytes。
• Tebibyte (TiB)：太比字节。1 TiB = 2⁴⁰ bytes。
• Pebibyte (PiB)：拍比字节。1 PiB = 2⁵⁰ bytes。
• Exbibyte (EiB)：艾比字节。1 EiB = 2⁶⁰ bytes。

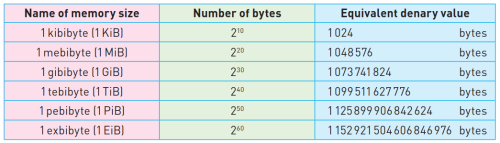
• 换算规则如下表所示：

1.3.2 Calculate the file size of an image file and a sound file, using information given 使用给定的信息计算图像文件和声音文件的文件大小

• Answers must be given in the units specified in the question 必须以问题中指定的单位给出答案
• Information given may include: 提供的信息可能包括：
- image resolution and colour depth图像分辨率和颜色深度
- sound sample rate, resolution and length of track声音采样率、分辨率和音轨长度

• 计算图像文件大小：
  • File size of an image = image resolution (in pixels) × colour depth (in bits)

• 计算声音文件大小：
  • File size of a mono sound file = sample rate (in Hz) × sample resolution (in bits) × length of sample (in seconds)
  • File size of a stereo sound file = sample rate (in Hz) × sample resolution (in bits) × length of sample (in seconds) × 2（因为是双声道）

1.3.3 Understand the purpose of and need for data compression 理解数据压缩的目的和需要

• Compression exists to reduce the size of the file 通过压缩以减小文件的大小
• The impact of this is, e.g.: 其影响是，例如：
- less bandwidth required需要更少的带宽
- less storage space required需要更少的存储空间
- shorter transmission time更短的传输时间

• Compression：压缩，指通过有损或无损的方式减少文件的大小。
  • 常见原因：
    • Save storage space on devices 节约设备存储空间
    • Reduce the time taken to stream a music or video file 减少在线播放音乐或视频的传输时间
    • Reduce the time taken to upload, download or transfer a file across a network 减少通过网络上传、下载或传输文件的时间
    • Use less bandwidth 使用更少的带宽
    • Reduces costs 减少成本
  • 分类：【参考1.3.4】
    • lossy compression有损压缩
    • lossless compression无损压缩

1.3.4 Understand how files are compressed using lossy and lossless compression methods 了解如何使用有损和无损压缩方法压缩文件

• Lossless compression reduces the file size without permanent loss of data, e.g. run length encoding (RLE) 无损压缩可减小文件大小而不会永久丢失数据，例如运行长度编码 (RLE) • Lossy compression reduces the file size by permanently removing data, e.g. reducing resolution or colour depth, reducing sample rate or resolution 有损压缩通过永久删除数据来减小文件大小，例如降低分辨率或颜色深度、降低采样率或分辨率

• Lossless compression：无损压缩，指减小文件大小的同时又不会损害文件完整性的压缩方式。如果后续有需要的话，可以恢复为与压缩前完全相同的形式。
  • 常见方法：Run length encoding（RLE）。将连续的重复字符写成number×character（重复次数×字符）的形式，以此减少使用的二进数值数量，减少文件大小。具体操作如下图所示：

• Lossy compression：有损压缩，指通过删除一部分文件内容以减少文件大小的压缩方式。文件内容删除后无法恢复，因此压缩后的文件无法再恢复为压缩前的形式。
  • 常见例子：JPEG、mp3、mp4等文件格式。
  • 常见方法：降低图像分辨率、降低色深、降低采样率、降低采样分辨率等。
  • 注意：虽然文件内容无法恢复，但由于人耳、人眼的试听限制，可能难以察觉压缩前后的区别，因此并不太影响人们对文件的使用。