CAIE AS and A Level CS revision - Unit 15 (2nd)

来自A level and IG Revision Wiki
跳到导航 跳到搜索

【点此返回复习要点目录】


如遇到公式加载异常，请刷新页面！

Unit 15 Hardware and Virtual Machines 硬件和虚拟机

15.1 Processors, Parallel Processing and Virtual Machines 处理器、并行处理和虚拟机

  • 大纲要求

CAIE-CS2nd-15.1要求.png


15.1.1 Show understanding of Reduced Instruction Set Computers (RISC) and Complex Instruction Set Computers (CISC) processors 了解精简指令集计算机 (RISC) 和复杂指令集计算机 (CISC) 处理器

Differences between RISC and CISC RISC和CISC的区别
Understand interrupt handling on CISC and RISC processors 了解 CISC 和 RISC 处理器的中断处理

  • 对control unit控制单元的控制与功能实现可以通过两种方式达成。
    • 一个是logic circuit逻辑电路，这种解决方式被称为hard-wired solution硬布线解决方案，机器代码直接由硬件处理和控制。
    • 另一个是采用microprogramming微程序。Firmware固件中有需要的microinstruction微指令或microcode微代码，控制单元通过这些微指令或代码来完成其功能。


  • Instruction set architecture：指令集架构，包括the instruction set指令集、the instruction format指令格式、the addressing modes寻址模式和the registers accessible by instructions指令可访问的寄存器。


  • Complex Instruction Set Computers (CISC)：复杂指令计算机，指采用大量指令，以降低使用高级语言的编译器写程序的难度。但由于指令很多，需要多次引用存储器，运行起来耗时较长，且有很多指令不常用，效率不高。
    • CISC采用microprogramming微程序处理，将一些常用的功能写成微指令，减少了编程者的工作。
    • 关于interrupt中断的处理： CISC是在一条指令执行结束后响应中断。
  • Reduced Instruction Set Computers (RISC)：精简指令计算机，指通过精减机器指令系统来减少硬件设计的复杂程度，提高指令执行速度。
    • RISC采用hard-wired control unit硬布线控制单元，多数由硬件控制，除了输入输出之外都从寄存器中读取，速度快。
    • 关于interrupt中断的处理：RISC 机器在一条指令执行的适当地方可以响应中断。可以考虑擦除没有全部完成的指令，处理完中断后重新开始这些指令；也可以考虑在处理器中创建新的单元存储当前数据，处理完中断后再读取这些数据并继续完成操作。
    • 存在Piping流水线操作。【参考15.1.2】


  • CISC和RISC的主要区别点如下表所示：
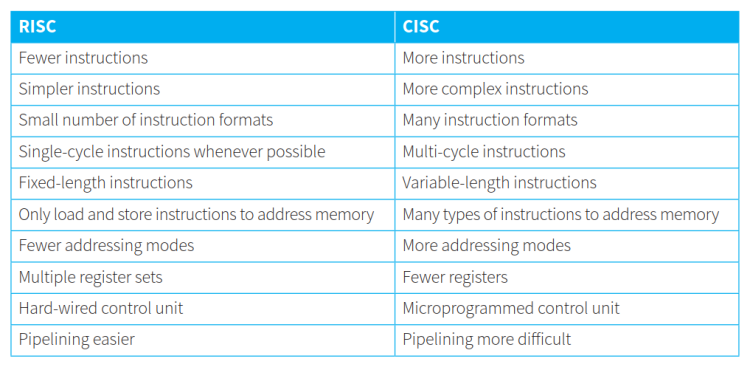
CAIE-CS2nd-15.1.1-1.png


15.1.2 Show understanding of the importance / use of pipelining and registers in RISC processors 理解 RISC 处理器中流水线和寄存器的重要性/使用

  • Piping：流水线操作，指用于指令执行的并行模式，可以节约时间，是RISC重要的设计原则之一。将指令分解成固定字长的独立单元，按照clock cycle同时、不间断地进行多条数据的并行处理。
    • 运行原理：比如如下图所示的fetch-decode-execute cycle五阶段模型中，第一个周期内，运行第一条指令的第一个阶段（1.1）。第二个周期内，运行第一条指令的第二个阶段（1.2）和第二条指令的第一个阶段（2.1）。以此类推。
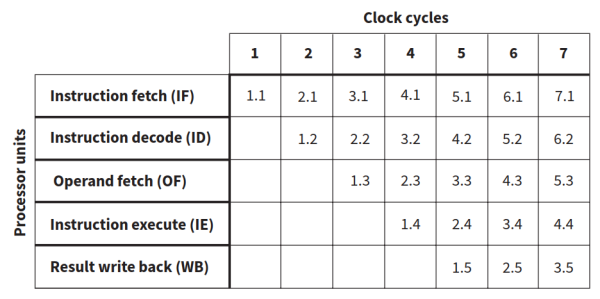
CAIE-CS2nd-15.1.2-1.png


  • 寄存器对RISC的作用：RISC简化了指令，将除了数据读入和输出之外的指令基本都存入了register寄存器内，从而可以实现指令的高速读取，提高运行速度。


15.1.3 Show understanding of the four basic computer architectures 展示对四种基本计算机体系结构的理解

SISD, SIMD, MISD, MIMD SISD、SIMD、MISD、MIMD

  • SISD：Single Instruction Stream Single Data Stream单指令单数据流。传统的顺序执行的单处理器计算机使用这种结构，其指令部件每次只对一条指令进行译码，并只对一个操作部件分配数据。示意图如下：
CAIE-CS2nd-15.1.3-1.png


  • SIMD：Single Instruction Stream Multiple Data Stream单指令流多数据流，采用一个指令流处理多个数据流。以vector processor阵列处理机为代表，其中包括多个重复的processing unit处理单元，由单一指令控制，按照同一指令流的要求为它们分配各自所需的不同数据。示意图如下：
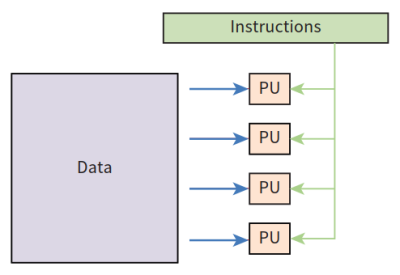
CAIE-CS2nd-15.1.3-2.png


  • MISD：Multiple Instruction Stream Single Data Stream多指令流单数据流，按多条不同指令的要求对同一数据流及其中间结果进行不同的处理。该结构一般仅在理论中讨论，现实中很少使用。
    • 一种可能的运用是fault-tolerant system容错系统，即运用不同的方法计算同一数据，如果结果一致则通过该结果。


  • MIMD：Multiple Instruction Stream Multiple Data Stream多指令流多数据流，可以同时执行多个指令流，这些指令流分别对不同数据流进行操作。
    • 现实当中的实例包括Massively parallel computer systems。【参考15.1.4】


15.1.4 Show understanding of the characteristics of massively parallel computers 了解大规模并行计算机的特性

  • 大规模并行计算机系统使用了MIMD结构，运行在不同computer unit计算机单元上的数据通过network网络相互传递，而非使用bus structure总线结构。
    • 另一种方式可考虑使用cluster computing集群计算（也可以称为server farm服务器群），将多台普通计算机联合起来达到和超级计算机类似的计算能力。


15.1.5 Show understanding of the concept of a virtual machine 展示对虚拟机概念的理解

Give examples of the role of virtual machines 举例说明虚拟机的作用
Understand the benefits and limitations of virtual Machines 了解虚拟机的优势和局限性

  • virtual machines：模拟机，是通过软件模拟的具有完整硬件系统功能的、运行在一个完全隔离环境中的完整计算机系统。在实体计算机中能够完成的工作在虚拟机中都能够实现。
    • 注意：虚拟机是一种软件，其进程直接与software interface软件界面连接，从而使用户软件通过虚拟机达到控制系统硬件完成相应功能的目的。示意图如下：
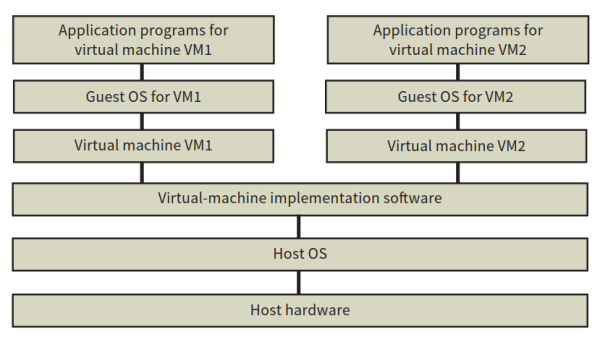
CAIE-CS2nd-15.1.5-1.png
      • 运行方式：在虚拟机上运行用户软件，调用虚拟机中模拟的操作系统，将指令传输出去。虚拟机通过虚拟机和计算机联系的软件将指令传递给计算机的操作系统，继而调用硬件完成指令。


  • 使用模拟机的好处：
    • 可以在同一计算机内使用多种操作系统。
    • 拥有大型计算机的公司可以向用户发送虚拟机，让用户将其作为服务器来访问。
  • 使用虚拟机的问题：
    • 实现虚拟机安装与使用需要耗费一定的时间与精力。
    • 通过虚拟机实现的性能会低于实体机本身的性能。


15.2 Boolean Algebra and Logic Circuits 布尔代数和逻辑电路

  • 大纲要求

CAIE-CS2nd-15.2要求.png


15.2.1 Produce truth tables for logic circuits including half adders and full adders 制作逻辑电路的真值表，包括半加器和全加器

May include logic gates with more than two inputs. 可能包含两个以上输入的逻辑门

  • half adder：半加器，指对两个输入数据位相加，输出一个sum bit和位（S）和carry bit进位（C），实现两个一位二进制数的加法运算电路。示意图如下：
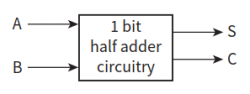
CAIE-CS2nd-15.2.1-1.png
    • 很多种电路组合都能够实现半加器的功能，其中NAND门和NOR门属于通用门，任何逻辑电路都可以通过仅使用NAND门或仅使用NOR门来实现。
    • 半加器的真值表如下所示：
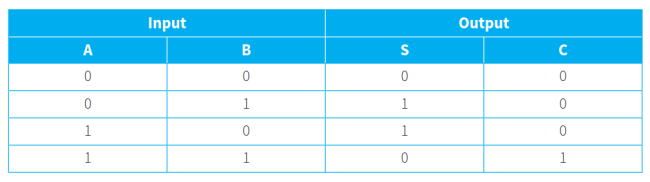
CAIE-CS2nd-15.2.1-2.png


  • full adder：全加器，指用门电路实现两个二进制数相加并求出和的组合线路。
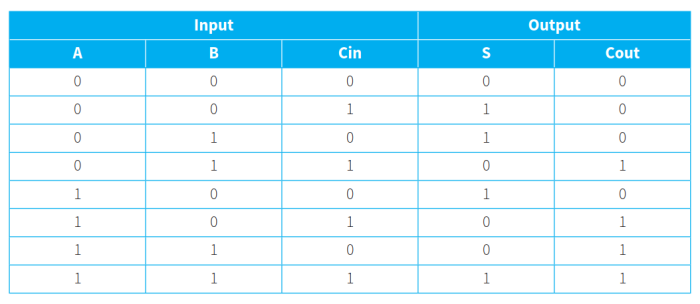
    • 全加器有三个输入位，包括两个需要相加的数位和一个上一步的进位（Cin）。输出位为一个sum bit和位（S）和carry bit进位（Cout）。一种可能的示意图如下：
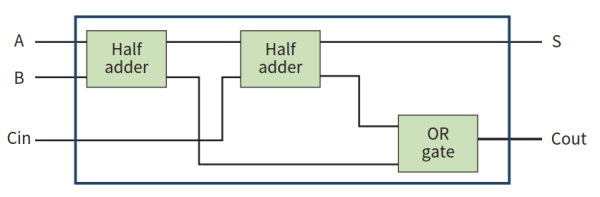
CAIE-CS2nd-15.2.1-3.png
    • 全加器的真值表如下所示：
CAIE-CS2nd-15.2.1-4.png


15.2.2 Show understanding of a flip-flop (SR, JK) 展示对触发器的理解（SR，JK）

Draw a logic circuit and derive a truth table for a flip-flop 画出逻辑电路并推导出触发器的真值表
Understand of the role of flip-flops as data storage elements 了解触发器作为数据存储元件的作用

  • combinational circuit：组合电路，指输出结果仅由输入的数据决定的电路。
  • sequential circuit：序列电路，指输出结果由输入的数据和上一次输出结果共同决定的电路。
    • flip-flop属于sequential circuit序列电路类型。


  • SR flip-flop：SR触发器，指根据set置位和reset复位输入的与非关系生成一个离散输出值的逻辑电路。
    • SR触发器逻辑电路示意图如下所示（使用NOR门表示）：
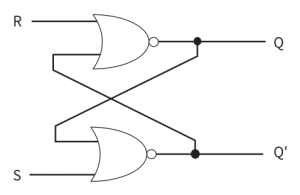
CAIE-CS2nd-15.2.2-1.png
    • SR触发器的真值表如下（使用NOR门表示）：
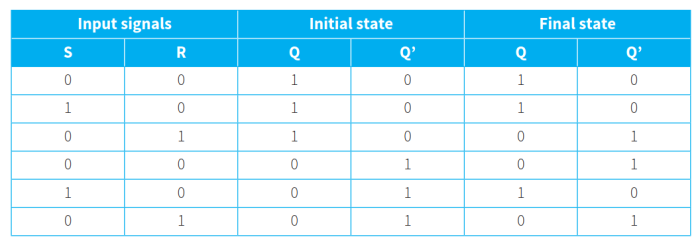
CAIE-CS2nd-15.2.2-2.png
      • Set state：设定状态，即Q=1且Q’=0时的状态（表中前三行初始状态）。这时的状态是稳定的，称为self-consistent自相一致的。
      • Unset state：非设定状态，即Q=0且Q’=1时的状态（表中后三行初始状态）。这时的状态是稳定的，称为self-consistent自相一致的。
      • Set操作：将状态变为set state时的操作，通过S=1且R=0实现。
      • Reset操作：将状态变为unset state时的操作，通过S=0且R=1实现。
      • 注意：真值表中不含有S=1且R=1的情况，因为这会导致Q和Q’均为0的无意义状态。因此现实中需要避免电路中同时接收S和R的输入信号。
    • SR触发器的作用：
      • 作为RAM的控件使用，因为其中存储的值可以发生改变。


  • JK flip-flop：JK触发器，指加入了clock时钟输入，能够完成置0、置1、保持和翻转功能的逻辑电路。
    • JK触发器逻辑电路示意图如下所示（a图为使用符号表示，b图为使用NAND门表示）：
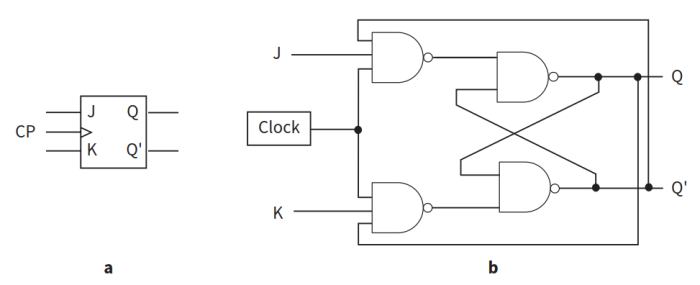
CAIE-CS2nd-15.2.2-3.png
    • JK触发器的真值表如下（使用NAND门表示）：
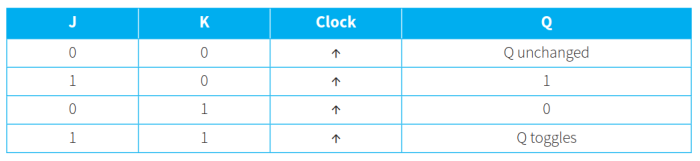
CAIE-CS2nd-15.2.2-4.png
      • J是set input置位输入，K是clear input清除输入。
    • JK触发器的作用：
      • 去除了SR触发器中可能出现的无意义输入情况和信号无法同时到位导致错误的情况，每个输入都能够得出数值。


15.2.3 Show understanding of Boolean algebra 展示对布尔代数的理解

Understand De Morgan’s laws. 了解德摩根定律。
Perform Boolean algebra using De Morgan’s laws. 使用德摩根定律进行布尔代数。
Simplify a logic circuit/expression using Boolean algebra 使用布尔代数简化逻辑电路/表达式

  • 布尔代数的运算法则如下表所示：
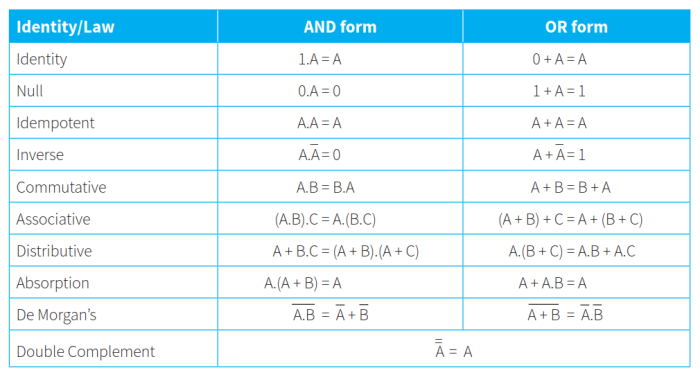
CAIE-CS2nd-15.2.3-1.png
    • De Morgan’s laws：德摩根法则，\(\overline{A.B}=\overline{A}+\overline{B}\)或\(\overline{A+B}=\overline{A}.\overline{B}\)。
    • 根据上面的运算法则，可以对逻辑运算式进行一定的简化。


  • 布尔代数式的提炼与表达：
    • 可根据真值表写出布尔代数式：
      • 提炼方法：查看真值表中总值为1的行。对于每行，将值为0的变量应用NOT运算，之后和值为1的变量进行AND运算。对于所有行，将每行写出的式子应用OR运算（有几行写几行）。
      • 例子：比如运用下表来写S的布尔代数式。S有两行的值为1。对于第二行，表达式为\(\overline{A}.B\)。对于第三行，表达式为\(A.\overline{B}\)。则\(S=\overline{A}.B+ A.\overline{B}\)。
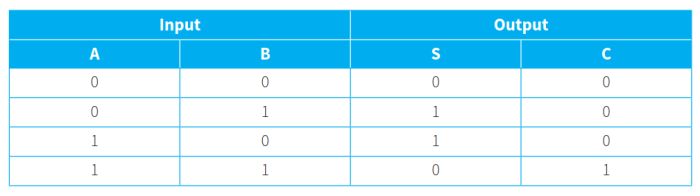
CAIE-CS2nd-15.2.3-2.png


    • 可根据逻辑电路图写出布尔代数式：
      • 提炼方法：按照电路图的逻辑运算写出相应的布尔表达式，并根据布尔运算法则进行化简。
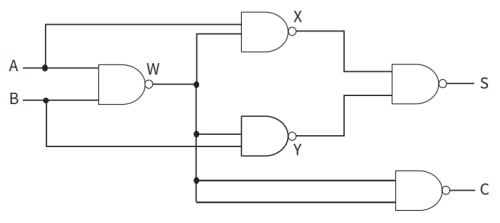
      • 例子：比如运用下图来写S的布尔代数式。根据真值表，\(W=\overline{A}.\overline{B}+ \overline{A}.B+A.\overline{B}\)。计算X时，将NAND拆为NOT(AND)运算。AND计算为\(A.(\overline{A}.\overline{B}+\overline{A}.B+A.\overline{B})=0+0+A.A.\overline{B}=A.\overline{B}\)。再进行NOT计算，根据德摩根法则，\(NOT(A.\overline{B})=\overline{A}+B\)，所以\(X=\overline{A}+B\)。同理可得\(Y=A+\overline{B}\)。所以对X和Y进行AND运算，得到\(X.Y=(\overline{A}+B).(A+\overline{B})\)，再进行NOT运算，根据德摩根法则，\(NOT(X.Y)=NOT[(\overline{A}+B).(A+\overline{B})]=\overline{A}.B+A.\overline{B}\)。所以\(S=\overline{A}.B+A.\overline{B}\)。
CAIE-CS2nd-15.2.3-3.png


15.2.4 Show understanding of Karnaugh maps (K-map) 展示对卡诺图（K-map）的理解

Understand of the benefits of using Karnaugh maps 了解使用卡诺图的好处
Solve logic problems using Karnaugh maps 使用卡诺图解决逻辑问题

  • Karnaugh maps (K-map)：卡诺图，是逻辑函数的一种图形表示，用于快速找出布尔代数式。
    • 使用卡诺图的分group组原则：
      • 仅考虑包含 1 的单元格。
      • Group组为行、列或矩形，相邻都是1则可考虑归为一组。
      • 组中包含的单元格数必须是 2、4、8 等2的次方数。
      • 每个组应尽可能大。
      • 组可以重叠，也可以按照首尾相接原则将首尾归为一组。
      • 如果单个单元格不能包含在任何组中，则将其视为一个组。
      • 对每个组确定代数式时，在组中保持恒定且值为1的输入值即为要找的代数式。若有多个不变的输入值，则按照AND关系连接。
      • 多个组代数式之间按照OR关系连接。
    • 确定布尔代数式的操作步骤：
      • 假设有以下的真值表：
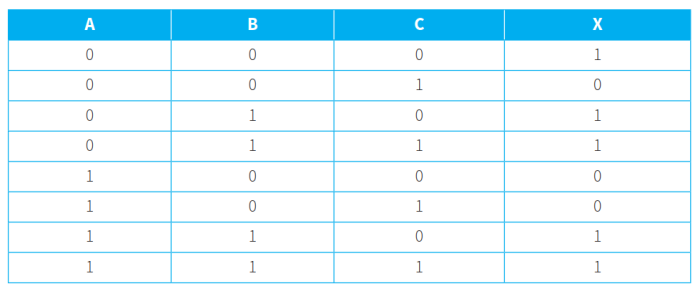
CAIE-CS2nd-15.2.4-1.png
      • 将上面的真值表转化为二维的卡诺图：
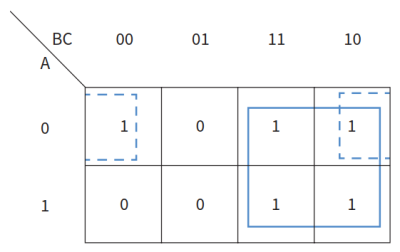
CAIE-CS2nd-15.2.4-2.png
      • 按照卡诺图分组原则，可画出两个组（实线组和虚线组）。
      • 实线组中，数值没有发生变化的是B，因此本组的布尔代数式为B。
      • 虚线组中，数值没有发生变化的是A和C（此时不变的数值都是0）。将两组数值变成1并按照AND连接，因此本组的布尔代数式为\(\overline{A}.\overline{C}\)。
      • 将两组用OR连接，得到最终的布尔代数式为\(\overline{A}.\overline{C}+B\)。


取自“http://81.70.248.142/index.php?title=CAIE_AS_and_A_Level_CS_revision_-_Unit_15_(2nd)&oldid=2753”