CAIE AS and A Level CS revision - Unit 18 (2nd)
跳到导航
跳到搜索
【点此返回复习要点目录】






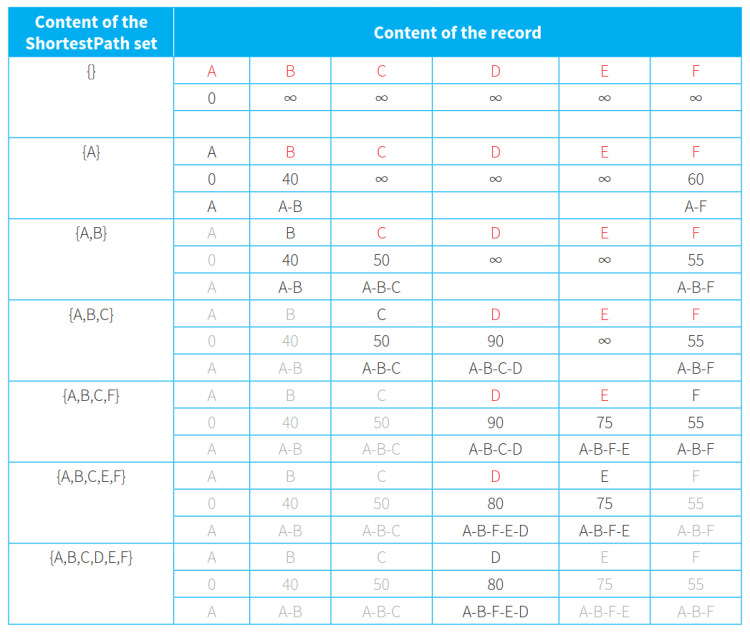
(表内最左列表示ShortestPath集,灰字节点代表已进入ShortestPath集不再考虑的节点,黑字节点代表正在判断最短路径的节点,红字代表仍处于RemainingNodes集里的节点)
如遇到公式加载异常,请刷新页面!
Unit 18 Artificial Intelligence (AI) 人工智能 (AI)
18.1 Artificial Intelligence (AI) 人工智能(AI)
- 大纲要求
18.1.1 Show understanding of how graphs can be used to aid Artificial Intelligence (AI) 了解如何使用图表来辅助人工智能 (AI)
Purpose and structure of a graph 图的目的和结构
Use A* and Dijkstra’s algorithms to perform searches on a graph 使用 A* 和 Dijkstra 算法在图上执行搜索
Candidates will not be required to write algorithms to set up, access, or perform searches on graphs 考生无需编写算法来设置、访问或执行图表搜索
- Artificial Intelligence (AI):人工智能,指使用计算机来完成目前人类能更加出色完成的一些任务。
- Graph:图,指node节点或vertice顶点的集合。每个节点有其名称,节点之间的连线称为edge边。相邻的两个节点称为neighbours邻居。
- 图可以分为unweighted graph无权重图和weighted graph有权重图两种。
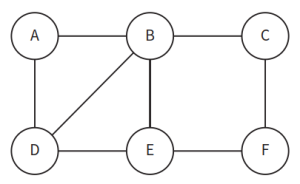
- unweighted graph:无权重图,指边上没有标签记录权重的图。如下图所示:
- 图可以分为unweighted graph无权重图和weighted graph有权重图两种。

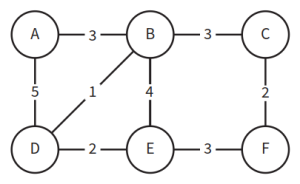
- weighted graph:有权重图,指边上有标签记录权重的图。边上的label标签中的数字是权重,代表从一个节点到另一个节点的距离。如下图所示:

- 图可以分为directed graph有方向图和indirect graph无方向图两种。
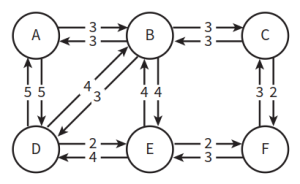
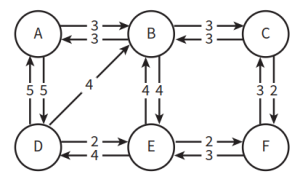
- directed graph:有方向图,指节点之间的连接有方向性。如果存在权重,那么不同方向的边的权重有可能不同。如下图所示:
- 图可以分为directed graph有方向图和indirect graph无方向图两种。

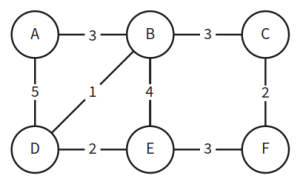
- indirect graph:无方向图,指节点之间的连接无方向性。如下图所示:

- 有时图的方向性会受到部分阻碍(一部分是单边通行),如下图所示:

- graph图结构的表达:除了画图表示之外,还可以采用adjacency matrix邻接矩阵或adjacency list邻接表来表示。
- adjacency matrix:邻接矩阵,指列出二维矩阵表格,行列交点处为节点间的关系。
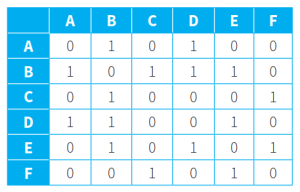
- 用adjacency matrix邻接矩阵表示无权重图:1表示两节点间存在边连接,0表示两节点间没有边连接。如下图所示:
- adjacency matrix:邻接矩阵,指列出二维矩阵表格,行列交点处为节点间的关系。


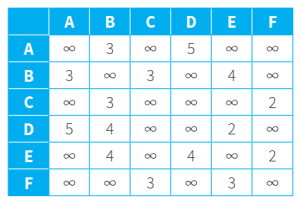
- 用adjacency matrix邻接矩阵表示有权重图:如果两节点间存在边连接,则行列交点处填入权重值;如果两节点间没有边连接,则行列交点处填入无穷大(∞)。如下图所示:


- adjacency list:邻接表,指列出节点和其相邻的邻居节点的列表。
- 用adjacency list邻接表表示无权重图:仅列出节点的邻居节点即可。如下图所示:
- adjacency list:邻接表,指列出节点和其相邻的邻居节点的列表。


- 用adjacency list邻接表表示有权重图:将节点和其权重一并列入表内。如下图所示:


- Dijkstra’s algorithms:戴克斯特拉算法使用类似广度优先搜索的方法,解决赋权图的单源最短路径问题。该算法通常用于在固定了一个顶点作为源结点后找到该顶点到图中所有其它结点的最短路径,产生一个最短路径树。
- 算法的逻辑思路:
- 准备阶段:
- 算法的逻辑思路:
- 识别路径开始的source node源节点(S)。
- 将ShortestPath最短路径集设置为空集。该集中将包含已经确定了最短路径的节点。
- 创建一个名为RemainingNodes剩余节点的集合,并将包括源节点(S)在内的所有节点放入其中,代表还没有确定最短路径的节点。
- 创建一个记录,用于存储当前节点名称、从源节点到该节点的距离值,以及从源节点到该节点的中转节点序列。
- 将源节点 S 的距离值设置为 0,其余节点的距离值设置为无穷大(代码中将其设置为非常大的数字)。
- 循环操作阶段:
- 在RemainingNodes集合里,挑选距离值最小的节点(N)。这意味着未被确定最短路径的节点中,均不可能有小于该距离值的路径选择了。
- 将此节点移动到ShortestPath集里,意味着已经为该节点确定了最短路径,其路径和距离值不再改动。
- 关注仍在RemainingNodes集里且与 N 相邻的每个节点(有路径相连的节点)。计算以N为前置出发点前往这些节点的距离总值(N的距离加本边上的距离值)。
- 将新计算出的距离总值与当前记录中存储的距离值进行比较,如果新值小于当前记录值,则将新值计入存储(代替掉旧值),并更新记录中的中转节点序列。
- 结束阶段:
- 当所有的点均进入ShortestPath最短路径集,意味着已经为所有节点找到了源节点到该节点的最短路径,算法结束。
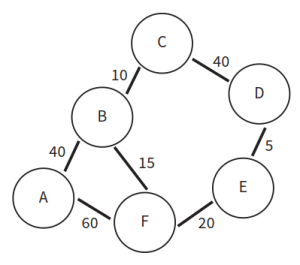
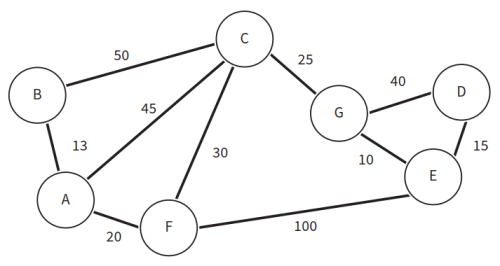
- Dijkstra算法例子:找出下图从源节点A到其他各节点的最短路径。算法参考如表格所示:


- 初始阶段,ShortestPath集为空集,RemainingNodes集里包含所有节点。源节点A的距离设置为0,其他节点的距离设置为无穷大。(第一行数据)
- 在RemainingNodes集里,A点的距离最短,将其放入ShortestPath集,其距离值不再改动。
- 考虑和A相邻的在RemainingNodes集里的两个节点B和F。以A的距离值0为基础,加上边值计算到B和F的距离值。得到A-B的距离值为40,A-F的距离值为60。
- 由于B节点的新值40小于旧值无穷大,更新B节点距离为40并记录新路径。F节点的新值60小于旧值无穷大,更新F节点距离为60并记录新路径。(第二行数据)
- A已进入ShortestPath集,不再考虑。其他距离值中,B节点的距离值最短,将其放入ShortestPath集,其距离值不再改动。
- 考虑和B相邻的在RemainingNodes集里的两个节点C和F。以B的距离值40为基础,加上边值计算到C和F的距离值,得到A-B-C的距离值为50,A-B-F的距离值为55。
- 由于C节点的新值50小于旧值无穷大,更新C节点距离为50并记录新路径。F节点的新值55小于旧值60,更新F节点距离为55并记录新路径。(第三行数据)
- A、B已进入ShortestPath集,不再考虑。其他距离值中,C节点的距离值最短,将其放入ShortestPath集,其距离值不再改动。
- 考虑和C相邻的在RemainingNodes集里的一个节点D。以C的距离值50为基础,加上边值计算到D的距离值,得到A-B-C-D的距离值为90。
- 由于D节点的新值90小于旧值无穷大,更新D节点距离为90并记录新路径。(第四行数据)
- A、B、C已进入ShortestPath集,不再考虑。其他距离值中,F节点的距离值最短,将其放入ShortestPath集,其距离值不再改动。
- 考虑和F相邻的在RemainingNodes集里的一个节点E。以F的距离值55为基础,加上边值计算到E的距离值,得到A-B-F-E的距离值为75。
- 由于E节点的新值75小于旧值无穷大,更新E节点距离为75并记录新路径。(第五行数据)
- A、B、C、F已进入ShortestPath集,不再考虑。其他距离值中,E节点的距离值最短,将其放入ShortestPath集,其距离值不再改动。
- 考虑和E相邻的在RemainingNodes集里的一个节点D。以E的距离值75为基础,加上边值计算到E的距离值,得到A-B-F-E-D的距离值为80。
- 由于D节点的新值80小于旧值90,更新D节点距离为80并记录新路径。(第六行数据)
- 将D节点放入ShortestPath集,其距离值不再改动。
- 此时,所有节点均已进入ShortestPath集,算法结束,记录中的距离值和路径即为最短路线的距离和具体线路。
- A* algorithm:A*算法,是一种静态网路中求解最短路径的直接搜索算法。该算法对Dijkstra’s algorithms进行了改进,当仅查询从一个节点到另一个节点的最短路径时,无需遍历所有节点,只需运算到目标节点为止。
- 注意:A*算法的改进点主要是增加了对当前节点到目标节点的估计值,选取尽量短的路径来探索,以提高算法效率。
- A*算法的操作流程:
- 准备阶段:
- 创建initial list初始列表、open list开放列表(正在考虑的节点)和closed list关闭列表(已检查完毕的节点)。
- 将图中每个节点的空记录插入到初始列表中。
- 将节点的 x 和 y 坐标存储在初始列表的每条记录中。
- 在初始列表的每条记录中将行进距离的值初始化为零。
- 创建一个look-up table查找表,其中包括具有直接连接道路的每对节点。
- 在表中存储每对节点沿该道路行驶的距离。
- 确定target node目标节点。
- 循环操作阶段:
- 将起点S加入开放列表。
- 找出 S 周围所有相邻的节点,将 S 设为相邻节点的parent node父节点,并将其加入开放列表。算出从 S 移动到该节点的总距离(记为 G)。
- 将S从开放列表中移除,进入关闭列表(已考虑完毕)。
- 对开放列表中的这些相邻节点进行其到目标节点的距离估计(比如可采用Manhattan distance曼哈顿距离估计,计算坐标间的最短距离),估计值记为H。
- 计算各个节点的总距离F=G+H。选择F值最小的节点,以此时的距离值为基础,重复上述找出相邻节点的操作。下一轮循环中需要注意的是:
- 如果相邻节点已经在关闭列表中,则直接忽略。
- 如果相邻节点不在开放列表中,则计算 G、H、F的值,为这些相邻节点设置好父节点(即当前考虑的节点),并将其加入开放列表。
- 如果相邻节点已经在开放列表中(即该节点已有自己的父节点),则比较从当前节点移动到该邻居是否能使其得到更小的 G 值。如果能,则把该相邻节点的父节点重设为当前节点,并更新其 G 和 F 值。如果不能,则保持原父节点不变。
- 完成对相邻节点的处理后,把当前节点从开放列表中移除,放入关闭列表(已经对该节点情况检查完毕)。
- 持续上述循环处理过程,直到相邻节点中F值最小的点恰好是目标节点,算法结束。记录中记下的具体路径和距离值F即为所求的最短路径。
- 准备阶段:
- A*算法例子:找出下图从起始节点A到目标节点D的最短路径。算法参考如下:

- 创建initial list初始列表、open list开放列表(正在考虑的节点)和closed list关闭列表(已检查完毕的节点)。
- 将起点A加入开放列表。
- 找出A周围所有相邻的节点B、C、F,将A设为B、C、F节点的父节点,并将这些节点加入开放列表。算出从A移动到这些相邻节点的距离。A-B距离为13,A-C距离为45,A-F距离为20。
- 将A从开放列表中移除,进入关闭列表。
- 对B、C、F节点进行其到目标节点D的距离估计。B-D估计距离为100,C-D估计距离为51,F-D估计距离为89。
- 计算B、C、F节点的总距离。B节点总距离为113,C节点总距离为96,F节点总距离为109。
- 选择总距离值最小的节点,即C节点。继续进行下一轮循环操作。
- 找出C周围所有相邻的节点F、G,将其加入开放列表。算出从C移动到这些相邻节点的距离。A-C-F距离为75,A-C-G距离为70。由于G没有父节点,则C成为G的父节点。F已有父节点A,则比较A-F和A-C-F的距离值大小,由于A-F的距离值更小,所以F的父节点保持A不变,距离仍是20。
- 将C从开放列表中移除,进入关闭列表。
- 对F、G节点进行其到目标节点D的距离估计。F-D估计距离为115,G-D估计距离为25。
- 计算F、G节点的总距离。F节点总距离为135,G节点总距离为95。
- 选择总距离值最小的节点,即G节点。继续进行下一轮循环操作。
- 找出G周围所有相邻的节点D、E,将其加入开放列表。算出从G移动到这些相邻节点的距离。A-C-G-D距离为110,A-C-G-E距离为80。由于D、E没有父节点,则G成为D、E的父节点。
- 将G从开放列表中移除,进入关闭列表。
- 对D、E节点进行其到目标节点D的距离估计。D-D估计距离为0,E-D估计距离为15。
- 计算D、E节点的总距离。D节点总距离为110,E节点总距离为95。
- 选择总距离值最小的节点,即E节点。继续进行下一轮循环操作。
- 找出E周围所有相邻的节点D,将其加入开放列表。算出从E移动到相邻节点的距离。A-C-G-E-D距离为95。D已有父节点G,则比较A-C-G-D和A-C-G-E-D的距离值大小,由于A-C-G-E-D的距离值更小,所以D的父节点变更为E,距离变更为95。
- 将E从开放列表中移除,进入关闭列表。
- 对D节点进行其到目标节点D的距离估计。D-D估计距离为0。
- 计算D节点的总距离。D节点总距离为95。
- 此时,总距离值最小的节点正是目标节点,算法结束。记录中存储的具体路径A-C-G-E-D以及距离值95,即为最短路径及其距离值。
18.1.2 Show understanding of how artificial neural networks have helped with machine learning 展示对人工神经网络如何帮助机器学习的理解
Show understanding of Deep Learning, Machine Learning and Reinforcement Learning and the reasons for using these methods. 展示对深度学习、机器学习和强化学习的理解以及使用这些方法的原因。
Understand machine learning categories, including supervised learning, unsupervised learning 了解机器学习类别,包括监督学习、无监督学习
- Machine learning:机器学习,指计算机会从大量的数据中学习,然后利用运行时获得的经验来改善自身的性能,不需要进行明确的编程。常见的机器学习分类如下:
- Supervised learning:监督学习。人们为计算机提供输入与输出,计算机逐渐探索出二者之间的联系,并在后续获得输入时,给出预测的输出。
- Unsupervised learning:无监督学习。计算机对原始资料进行分类,找出其潜在类别规则,将相似的数据聚在一起(但不关心这些数据的具体内容)。
- Reinforcement learning:强化学习。计算机以“试错”的方式进行学习,通过与环境进行交互,如果行为能够获得奖励则积累了正确行动的经验,最终目标是使计算机获得最多的奖励。
- Deep learning:深度学习。计算机通过学习样本数据的内在规律和表示层次,最终实现机器能够像人一样具有分析学习能力,能够识别文字、图像和声音等数据。
- 深度学习可通过对神经网络中的隐藏层不断进行修正实现。【参考18.1.3】
18.1.3 Show understanding of back propagation of errors and regression methods in machine learning 展示对机器学习中错误和回归方法的反向传播的理解
- Regression:回归分析,指判断变量间是否存在相关关系。如果存在相关性,则可以根据已输入的数据值,预测某些量的输出值。
- 注意:线性关系是回归分析中最简单的一种关系。但现实中的变量关系可能会更复杂,比如指数关系等。
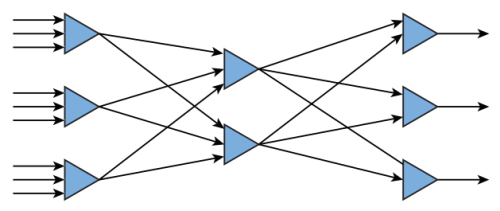
- Artificial neural network:人工神经网络,指由大量的node节点(或称artificial neuron人工神经元)相互联接构成的类似人脑神经的网络体系。示意图如下(三角形代表节点,箭头代表信息流向):

- 一个节点可以接收一个或多个输入,并可以向一个或多个节点输出。
- 神经网络的最左端是输入端,最右端是输出端,中间则是hidden layer隐藏层。
- 传送路径上带有weighting factor权重要素,当有多个输入时,根据权重,通过activation function激励函数算出输出值。权重和激励函数是可调节的,通过不断修正权重大小和激励函数的计算方式,可以逐渐实现系统的最佳预测能力。
- Back propagation of errors:误差反向传播,指通过实际输出值与预测输出值之间的误差,对神经网络不断修正的算法。可看作是神经网络学习训练的过程。
- 训练过程:
- 人们通过监督学习,获得了变量之间可能存在的关系。
- 人们将输入值输入模型,获得预测的输出值。
- 将预测输出值与现实中实际的输出值进行比对,确定误差。
- 不断调节权重或函数,使误差逐渐缩小,预测输出值逐渐靠近现实中的实际输出值。
- 神经网络的预测精准程度逐渐上升。
- 误差反向传播的缺点:可能要花费较长时间来训练和修正。
- 训练过程:
