CAIE AS and A Level CS revision - Unit 19 (2nd)

【点此返回复习要点目录】

如遇到公式加载异常，请刷新页面！

Unit 19 Computational thinking and problem-solving 计算思维和问题解决

19.1 Algorithms 算法

• 大纲要求

19.1.1 Show understanding of linear and binary searching methods 展示对线性和二分搜索方法的理解

Write an algorithm to implement a linear search 编写算法实现线性搜索
Write an algorithm to implement a binary search 编写算法实现二分查找
The conditions necessary for the use of a binary search 使用二分查找的必要条件
How the performance of a binary search varies according to the number of data items 二分查找的性能如何根据数据项的数量而变化

• linear search：线性搜索。
  • 线性搜索的思路：被查找序列按顺序从头到尾一个一个元素查看，如果找到目标，则输出目标所在位置。
  • 线性搜索的伪代码【参考10.2.4】。
• binary search：二分查找。
  • 二分查找的必要条件：被查找序列是有序的。
  • 二分查找的思路：首先必须保证被查找序列是有序的，如果无序则进行排序或选择其他搜索方法。如果有序，则每次搜索时，将被查找序列一分为二，如果目标值位于前半部分，则仅保留前半部分数据作为下一次查找序列；反之，如果目标值位于后半部分，则仅保留后半部分数据作为下一次查找序列。重复上述操作，直至找到目标值为止（如果目标值不在序列中，则输出错误信息）。
  • 二分查找的伪代码：

Found ← FALSE //定义一个是否找到的标记，默认值为FALSE未找到，如果找到则修改其状态为TRUE
SearchFailed ← FALSE //定义一个目标数据是否不在序列中的标记，默认值为FALSE查找暂未失败，如果查找失败则修改其状态为TRUE
First ← 0 //查找段的首个元素所在位置，初始位置为数组中的第0位
Last ← MaxItems – 1 //查找段的首个元素所在位置，初始位置为数组中的第（MaxItems-1）位
WHILE NOT Found AND NOT SearchFailed DO //如果此时既没有找到，也没有查找失败，则进入循环
　　Middle ← (First + Last) DIV 2 //确定查找段中间的元素
　　IF List[Middle] = SearchItem
　　　THEN
　　　　Found ← TRUE //如果中间元素恰好是目标数据，则确认找到
　　　ELSE
　　　　IF First >= Last //此处有等号，是表示虽然序列内仅剩一个元素，但由于上面已经判定该元素不是查找的目标数据，所以查找实际已经失败，简化了一次循环
　　　　　THEN
　　　　　　SearchFailed ← TRUE //如果序列已经全部查找完毕或仅剩的一个元素也非目标数据，则确认查找失败
　　　　　ELSE
　　　　　　IF List[Middle] > SearchItem //如果中间元素大于目标数据，则目标数据必然位于前半段
　　　　　　　THEN
　　　　　　　　Last ← Middle - 1 //将查找段的后部缩短，查找段变为原来的一半
　　　　　　　ELSE //如果中间元素小于目标数据，则目标数据必然位于后半段
　　　　　　　　First ← Middle + 1 //将查找段的前部缩短，查找段变为原来的一半
　　　　　　ENDIF
　　　　ENDIF
　　ENDIF
ENDWHILE
IF Found = TRUE //全部循环结束，如果找到
　THEN
　　OUTPUT Middle //输出目标数据在原序列的位置
　ELSE //全部循环结束，没有找到
　　OUTPUT "Item not present in array" //输出错误信息
ENDIF

• • 二分查找的效率：二分查找每次缩减为原查找序列的一半，因此复杂度平均为O(log(n))，最差情况下为O(n)。在数据较多时，二分查找比线性搜索要快。

19.1.2 Show understanding of insertion sort and bubble sort methods 展示对插入排序和冒泡排序方法的理解

Write an algorithm to implement an insertion sort 编写算法实现插入排序
Write an algorithm to implement a bubble sort 编写算法实现冒泡排序
Performance of a sorting routine may depend on the initial order of the data and the number of data items 排序例程的性能可能取决于数据的初始顺序和数据项的数量

• insertion sort：插入排序。
  • 插入排序的思路：类似扑克牌抽牌排序的方法。将要排序的数组分为已排序（前部）和未排序（后部）两部分，每次从未排序部分按顺序取出一个数据作为当前数据，与已排序的部分进行一一比对，直到找到合适的位置，将后面的所有元素统一向后移一位，然后将该数据插入当前位置。
  • 插入排序的伪代码：

FOR Pointer ← 1 TO NumberOfitems – 1 //由位于数组第1位的数据开始检查（第0位的数据自动成为已排序序列中的首项，无需检查）
　　ItemToBeInserted ← List[Pointer] //将当前的数据设定为要插入的数据
　　CurrentItem ← Pointer – 1 //当前指向要插入数据所处位置的前一项数据（已排序序列的最后一项数据）
　　WHILE (List[CurrentItem] > ItemToBeInserted) AND (CurrentItem > –1) DO //当前指向的数据大于插入项且还没有回溯到已排序序列的首项时，进入循环
　　　　List[CurrentItem + 1] ← List[CurrentItem] //将前一项的数据后移一位
　　　　CurrentItem ← CurrentItem – 1 //再往前查看一项的数据（当前指向的数据前移一位），准备下一轮循环
　　ENDWHILE
　　List[CurrentItem + 1] ← ItemToBeInserted //将数据插入到合适的位置（由于退出循环前CurrentItem做了-1的运算，因此合适的位置应该+1还原）
NEXT Pointer

• • 插入排序的效率：插入排序的复杂度平均及最差情况（最差情况为完全逆序）为O(n2)，最优情况（最优情况为完全顺序）下为O(n)。因此插入排序不适合处理数据量比较大的序列排序。

• Bubble sort：冒泡排序。
  • 冒泡排序的思路：依次检查数组中相邻的元素，如果顺序错误则将二者进行交换，直至完全排好顺序不再发生交换为止。
  • 冒泡排序的伪代码【参考10.2.4】。
  • 冒泡排序的效率：平均复杂度为O(n²)，经过优化后的冒泡排序复杂度最优情况（最优情况为完全顺序）下可达到O(n)，但最差情况（最差情况为完全逆序）下仍为O(n²)。

19.1.3 Show understanding of and use Abstract Data Types (ADT) 展示对抽象数据类型 (ADT) 的理解和使用

Write algorithms to find an item in each of the following: linked list, binary tree 编写算法以在以下各项中找到一项：链表、二叉树
Write algorithms to insert an item into each of the following: stack, queue, linked list, binary tree 编写算法以将项插入以下各项：堆栈、队列、链表、二叉树
Write algorithms to delete an item from each of the following: stack, queue, linked list 编写算法从以下各项中删除一项：堆栈、队列、链表
Show understanding that a graph is an example of an ADT. Describe the key features of a graph and justify its use for a given situation 理解图是 ADT 的一个例子。描述图的主要特征并证明其在给定情况下的用途
Candidates will not be required to write code for this structure. 考生无需为此结构编写代码。

• Abstract Data Types (ADT)：抽象数据类型。【参考10.4】
• 关于linked list链表的一系列操作的代码：
  • 创建一个新链表：

CONSTANT NullPointer = –1 //定义空指针为-1（此时数组首位为0）
TYPE ListNode //定义一个记录类型，来存放数据与对应的指针
　　DECLARE Data: STRING
　　DECLARE Pointer: INTEGER
ENDTYPE
DECLARE StartPointer: INTEGER
DECLARE FreeListPtr: INTEGER
DECLARE List: ARRAY[0 : 6] OF ListNode
PROCEDURE InitialiseList
　　StartPointer ← NullPointer //设定开始指针为空
　　FreeListPtr ← 0 //设定自由列表的初始位置为0
　　FOR Index ← 0 TO 5 //将各记录中的指针连接起来形成链表
　　　　List[Index].Pointer ← Index + 1 //第Index位数据对应的指针指向第Index+1位，形成连接
　　NEXT Index
　　List[6].Pointer ← NullPointer //最后一位数据对应的指针指向空位
ENDPROCEDURE

• • 向已排序的链表中插入一个新数据：

PROCEDURE InsertNode(NewItem)
　　IF FreeListPtr <> NullPointer //如果自由链表中还存在未分配的内存（没有指向空指针）
　　　THEN
//以下代码是从FreeListPtr中取出一个空内存并存入数据
　　　　NewNodePtr ← FreeListPtr //NewNodePtr指向自由链表中的一个节点（FreeListPtr指向的地址），用于处理新插入的数据
　　　　List[NewNodePtr].Data ← NewItem //将要插入的数据值放入NewNodePtr节点记录的Data项中
　　　　FreeListPtr ← List[FreeListPtr].Pointer //FreeListPtr指向下一个空内存地址（指向FreeListPtr指向的地址），意味着去掉了一个自由链表中的空内存

//以下代码是为待插入的数据单元寻找合适的位置
　　　　ThisNodePtr ← StartPointer //使用ThisNodePtr指向当前待处理单元的地址。从链表最开始的单元位置处理，使ThisNodePtr指向链表的首项
　　　　PreviousNodePtr ← NullPointer //待处理单元的前一项指针指向的地址，一开始默认为空指针（在起始指针前）
　　　　WHILE ThisNodePtr <> NullPointer //如果当前待处理单元不是最后一项（指向的不是空指针）
　　　　 AND List[ThisNodePtr].Data < NewItem DO //并且当前待处理单元的数值小于新插入的数值，则进入循环
　　　　　　PreviousNodePtr ← ThisNodePtr //将PreviousNodePtr的指针指向当前待处理单元（以防下个位置就是要插入的地方，记下位置方便连接），使其变为“前一项”以腾出ThisNodePtr指向的地址位置，引入下一个数据单元的分析
　　　　　　ThisNodePtr ← List[ThisNodePtr].Pointer //将当前待处理单元指向的下一项地址赋给ThisNodePtr，使其成为新的待处理单元
　　　　ENDWHILE

//由于是有序列表，此时PreviousNodePtr记录的就是新数据应该插入的合适位置（因为当前待处理单元ThisNodePtr指向的地址是不合适的才退出循环，而前一项PreviousNodePtr指向的地址正好是合适的最后一项）
　　　　IF PreviousNodePtr = StartPointer //如果待插入点为首项
　　　　　THEN
　　　　　　List[NewNodePtr].Pointer ← StartPointer //新数据的指针指向原起始指针指向的地址（和第二项进行连接）
　　　　　　StartPointer ← NewNodePtr //起始指针指向新插入的数据，承认其是链表的首项
　　　　 ELSE //如果待插入点不是首项
　　　　　　List[NewNodePtr].Pointer ← List[PreviousNodePtr].Pointer //新数据的指针指向PreviousNodePtr指向的原地址（和后一项连接）
　　　　　　List[PreviousNodePtr].Pointer ← NewNodePtr //前一项PreviousNodePtr的指针指向新数据单元NewNodePtr（和前一项连接）
　　　　ENDIF
　　ENDIF
ENDPROCEDURE

• • 从已排序的链表中查找一个数据的位置：

FUNCTION FindNode(DataItem) RETURNS INTEGER //输入一个数据，返回一个指针地址
　　CurrentNodePtr ← StartPointer //使用CurrentNodePtr指向当前待处理单元的地址。从链表最开始的单元位置处理，使CurrentNodePtr指向链表的首项
　　WHILE CurrentNodePtr <> NullPointer //如果当前待处理单元不是最后一项（指向的不是空指针）
　　 AND List[CurrentNodePtr].Data <> DataItem DO //并且当前待处理单元的数值并非要找的目标数值，则进入循环
　　　　CurrentNodePtr ← List[CurrentNodePtr].Pointer //使待处理单元的指针指向待处理单元指针指向的下一项（使待处理单元向下顺移）
　　ENDWHILE
　　RETURN CurrentNodePtr //如果当前待处理单元的数值正是要找的数值，则会跳出上面的循环，因此说明CurrentNodePtr指向的地址位置正是要返回的地址，输出即可（如果查不到相关数值，CurrentNodePtr会指向最后一项所指向的地址，即空指针）
ENDFUNCTION

• • 从已排序的链表中删除一个数据：

PROCEDURE DeleteNode(DataItem)
　　ThisNodePtr ← StartPointer //使用ThisNodePtr指向当前待处理单元的地址。从链表最开始的单元位置处理，使ThisNodePtr指向链表的首项
　　WHILE ThisNodePtr <> NullPointer //如果当前待处理单元不是最后一项（指向的不是空指针）
　　 AND List[ThisNodePtr].Data <> DataItem DO //并且当前待处理单元的数值并非要找的目标数值，则进入循环
　　　　PreviousNodePtr ← ThisNodePtr //将PreviousNodePtr的指针指向当前待处理单元（以防下个位置就是要删除的地方，记下位置方便连接），使其变为“前一项”以腾出ThisNodePtr指向的地址位置，引入下一个数据单元的分析
　　　　ThisNodePtr ← List[ThisNodePtr].Pointer //使待处理单元的指针指向待处理单元指针指向的下一项（使待处理单元向下顺移）
　　ENDWHILE

//跳出循环后，ThisNodePtr指向的位置就是待删除的节点位置（唯一的例外就是没找到数值，会返回空指针）
　　IF ThisNodePtr <> NullPointer //已找到待删除的节点（并非空指针）
　　　THEN
　　　　IF ThisNodePtr = StartPointer //如果待删除的节点是起始节点
　　　　　THEN
　　　　　　StartPointer ← List[StartPointer].Pointer //将起始指针指向起始节点指向的地址（起始指针移到第二项，则相当于去掉了首节点）
　　　　 ELSE
　　　　　　List[PreviousNodePtr].Pointer ← List[ThisNodePtr].Pointer //PreviousNodePtr指向的地址修改为当前待删除结点指向的地址（相当于跨过了待删除结点）
　　　　ENDIF
　　　　List[ThisNodePtr].Pointer ← FreeListPtr //将删除节点的指针指向自由链表的尾部，将删除节点连接到自由链表内
　　　　FreeListPtr ← ThisNodePtr //自由链表的尾部指针后移一位，表示空内存位置又多了一个
　　ENDIF
ENDPROCEDURE

• • 输出链表中的所有数据：

PROCEDURE OutputAllNodes
　　CurrentNodePtr ← StartPointer //使用CurrentNodePtr指向当前待处理单元的地址。从链表最开始的单元位置处理，使CurrentNodePtr指向链表的首项
　　WHILE CurrentNodePtr <> NullPointer DO //如果当前待处理单元不是最后一项（指向的不是空指针）
　　　　OUTPUT List[CurrentNodePtr].Data //输出当前待处理单元内存储的数据
　　　　CurrentNodePtr ← List[CurrentNodePtr].Pointer //使待处理单元的指针指向待处理单元指针指向的下一项（使待处理单元向下顺移）
　　ENDWHILE
ENDPROCEDURE

• 关于binary trees二叉树的一系列操作的代码：
  • Binary trees：二叉树，指仅有两个子分支的树结构。
    • 二叉树最上层为根节点，下有left subtree左子树与right subtree右子树。每个小结构中，上部的是parent node父节点，下部的称为child node子节点，同级的可称为sibling node兄弟节点。如果该节点之下没有子树结构，则可称为leaf node叶节点。示意图如下所示：

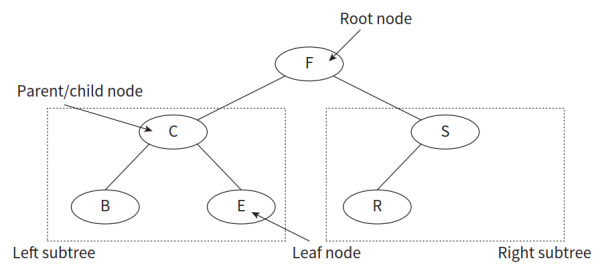
• • • 在代码中，可用记录类型的数组结构表示二叉树，每个记录中包括数值、左指针、右指针三部分。
  • 创建一个新二叉树：

CONSTANT NullPointer = –1 //将空指针设定为-1
TYPE TreeNode //用记录类型来设置二叉树的各个节点
　　DECLARE Data: STRING
　　DECLARE LeftPointer: INTEGER
　　DECLARE RightPointer: INTEGER
ENDTYPE
DECLARE RootPointer: INTEGER
DECLARE FreePtr: INTEGER
DECLARE Tree: ARRAY[0 : 6] OF TreeNode
PROCEDURE InitialiseTree
　　RootPointer ← NullPointer //设置根节点
　　FreePtr ← 0 //设定自由列表的初始位置为0
　　FOR Index ← 0 TO 5
　　　　Tree[Index].LeftPointer ← Index + 1 //第Index位数据对应的左指针指向第Index+1位，形成连接
　　NEXT Index
　　Tree[6].LeftPointer ← NullPointer //最后一位数据对应的左指针指向空位
ENDPROCEDURE

• • 向二叉树中插入一个新数据：

PROCEDURE InsertNode(NewItem)
　　IF FreePtr <> NullPointer //如果自由链表中还存在未分配的内存（没有指向空指针）
　　　THEN //以下代码是从FreePtr中取出一个空内存并存入数据
　　　　NewNodePtr ← FreePtr //NewNodePtr指向自由链表中的一个节点（FreePtr指向的地址），用于处理新插入的数据
　　　　FreePtr ← Tree[FreePtr].LeftPointer //FreePtr指向下一个空内存地址（指向FreePtr指向的地址），意味着去掉了一个自由链表中的空内存
　　　　Tree[NewNodePtr].Data ← NewItem //将要插入的数据值放入NewNodePtr节点记录的Data项中
　　　　Tree[NewNodePtr].LeftPointer ← NullPointer //将左指针设定为空指针（暂时没有左子树）
　　　　Tree[NewNodePtr].RightPointer ← NullPointer //将右指针设定为空指针（暂时没有右子树）

//以下代码是为待插入的数据单元寻找合适的位置
　　　　IF RootPointer = NullPointer //如果根节点为空指针（意味着这是一个empty binary tree空二叉树）
　　　　　THEN
　　　　　　RootPointer ← NewNodePtr //空二叉树时，将插入的数据单元设定为根节点（根节点的指针指向新数据单元）
　　　　 ELSE //如果这不是空二叉树，则需要确定具体的插入位置
　　　　　　ThisNodePtr ← RootPointer //使用ThisNodePtr指向当前待处理单元的地址。从二叉树的根节点位置开始处理，使ThisNodePtr指向根节点
　　　　　　WHILE ThisNodePtr <> NullPointer DO //如果当前节点不是叶节点（不指向空指针）
　　　　　　　　PreviousNodePtr ← ThisNodePtr//将PreviousNodePtr的指针指向当前待处理单元（以防下个位置就是要插入的地方，记下位置方便连接），同时也腾出ThisNodePtr以记录后续地址
　　　　　　　　IF Tree[ThisNodePtr].Data > NewItem //如果要插入的数据小于当前待处理单元的数据，则进入左子树
　　　　　　　　　THEN
　　　　　　　　　　TurnedLeft ← TRUE //进入左子树的标记设置为TRUE
　　　　　　　　　　ThisNodePtr ← Tree[ThisNodePtr].LeftPointer //ThisNodePtr指针指向该节点左指针指向的节点，处理下一个数据单元
　　　　　　　　 ELSE
　　　　　　　　　　TurnedLeft ← FALSE //进入左子树的标记设置为FALSE（说明进入右子树）
　　　　　　　　　　ThisNodePtr ← Tree[ThisNodePtr].RightPointer //ThisNodePtr指针指向该节点右指针指向的节点，处理下一个数据单元
　　　　　　　　ENDIF
　　　　　　ENDWHILE

//当跳出循环时，ThisNodePtr应为-1（即一路到了叶节点位置）。因此前一项的PreviousNodePtr记录下的地址应该是新数据应该连接的父节点位置
　　　　　　IF TurnedLeft = TRUE //如果前一步操作是进入左子树
　　　　　　　THEN
　　　　　　　　Tree[PreviousNodePtr].LeftPointer ← NewNodePtr //PreviousNodePtr的左指针连接NewNodePtr
　　　　　　 ELSE //如果前一步操作是进入右子树
　　　　　　　　Tree[PreviousNodePtr].RightPointer ← NewNodePtr //用PreviousNodePtr的右指针连接NewNodePtr
　　　　　　ENDIF
　　　　ENDIF
　　ENDIF
ENDPROCEDURE

• • 从二叉树中查找一个数据的位置：

FUNCTION FindNode(SearchItem) RETURNS INTEGER //输入一个数据，返回一个指针地址
　　ThisNodePtr ← RootPointer //使用ThisNodePtr指向当前待处理单元的地址。从二叉树最开始的单元位置处理，使ThisNodePtr指向根节点
　　WHILE ThisNodePtr <> NullPointer //如果当前节点不是叶节点（不指向空指针）
　　 AND Tree[ThisNodePtr].Data <> SearchItem DO //并且当前待处理单元的数值不是要找的数据，则进入循环（如果就是要找的数据，直接跳出循环）
　　　　IF Tree[ThisNodePtr].Data > SearchItem //如果要插入的数据小于当前待处理单元的数据，则进入左子树
　　　　　THEN
　　　　　　ThisNodePtr ← Tree[ThisNodePtr].LeftPointer //ThisNodePtr指针指向该节点左指针指向的节点，处理下一个数据单元
　　　　 ELSE //如果要插入的数据大于当前待处理单元的数据，则进入右子树
　　　　　　ThisNodePtr ← Tree[ThisNodePtr].RightPointer //ThisNodePtr指针指向该节点右指针指向的节点，处理下一个数据单元
　　　　ENDIF
　　ENDWHILE
　　RETURN ThisNodePtr //跳出循环时，ThisNodePtr就是要找的数据位置，输出即可（如果查不到该数据，则ThisNodePtr是空指针，证明已经遍历到了叶节点仍无要找的数据）
ENDFUNCTION

• 关于Stack栈的一系列操作的代码：
  • Stack：栈，指遵循先进后出的数组。【参考10.4.2】
    • 注意：BaseOfStackPointer始终指向数组的第0位，而TopOfStackPointer则随着数据进出而变动。当栈为空时，TopOfStackPointer值为-1。
  • 创建一个栈：

CONSTANT EMPTYSTRING = ""
CONSTANT NullPointer = –1 //定义空指针为-1（此时数组首位为0）
CONSTANT MaxStackSize = 8 //定义栈的大小
DECLARE BaseOfStackPointer: INTEGER //定义栈的底指针
DECLARE TopOfStackPointer: INTEGER //定义栈的顶指针
DECLARE Stack: ARRAY[1 : MaxStackSize – 1] OF STRING
PROCEDURE InitialiseStack
　　BaseOfStackPointer ← 0 //设置底指针指向最下方的数组单元（第0位）
　　TopOfStackPointer ← NullPointer //设置顶指针为空（即此时是空栈）
ENDPROCEDURE

• • 向栈中压入一个新数据：

PROCEDURE Push(NewItem)
　　IF TopOfStackPointer < MaxStackSize – 1 //如果栈内还有剩余空间
　　　THEN
　　　　TopOfStackPointer ← TopOfStackPointer + 1 //顶指针上移一位，指向新的数组位置
　　　　Stack[TopOfStackPointer] ← NewItem //将新数据存入当前指向的数组位置
　　ENDIF
ENDPROCEDURE

• • 从栈中弹出一个数据：

FUNCTION Pop() //无需参数输入，但会返回需要弹出的数据
　　DECLARE Item: STRING
　　Item ← EMPTYSTRING //将要弹出的数据变量初始化为空
　　IF TopOfStackPointer > NullPointer //如果栈内有数据（不是空栈）
　　　THEN
　　　　Item ← Stack[TopOfStackPointer] //要弹出的数据为顶指针指向的数组位置所存储的数据
　　　　TopOfStackPointer ← TopOfStackPointer – 1 //顶指针下移一位，意味着将栈中存储数据的位置缩减一位
　　ENDIF
　　RETURN Item //返回要弹出的数据。如果是空栈则返回空白字符串
ENDFUNCTION

• 关于Queue队列的一系列操作的代码：
  • Queue：队列，指遵循先进先出的数组。【参考10.4.2】
    • 注意：FrontOfQueuePointer始终指向队列中的第1个数据（即下一个要弹出的数据单元），而EndOfQueuePointer始终指向队列中的最后一个数据（即下一个要插入的数据单元之前）。
    • 注意：要注意queue with wrap-round循环队列的情况。
  • 创建一个队列：

CONSTANT EMPTYSTRING = ""
CONSTANT NullPointer = -1 //定义空指针为-1（此时数组首位为0）
CONSTANT MaxQueueSize = 8 //定义队列的大小
DECLARE FrontOfQueuePointer: INTEGER //定义队列的首指针
DECLARE EndOfQueuePointer: INTEGER //定义队列的尾指针
DECLARE NumberInQueue: INTEGER //定义一个变量来表示队列中的数据个数
DECLARE Queue: ARRAY[0 : MaxQueueSize – 1] OF STRING
PROCEDURE InitialiseQueue
　　FrontOfQueuePointer ← NullPointer //设置首指针为空
　　EndOfQueuePointer ← NullPointer //设置尾指针为空
　　NumberInQueue ← 0 //当前队列中的数据个数为0（初始化）
ENDPROCEDURE

• • 向队列中加入一个新数据：

PROCEDURE AddToQueue(NewItem)
　　IF NumberInQueue < MaxQueueSize //如果队列内还有剩余空间
　　　THEN
　　　　EndOfQueuePointer ← EndOfQueuePointer + 1 //尾指针加1，为队列增加一个存储位置
　　　　IF EndOfQueuePointer > MaxQueueSize – 1 //如果当前尾指针超过了队列数组的最大位置，则考虑循环队列（如果没超则跳过此处的代码，按照正常情况在尾部增加数据）
　　　　　THEN
　　　　　　EndOfQueuePointer ← 0 //将尾指针指向数据首项，形成循环队列
　　　　ENDIF
　　　　Queue[EndOfQueuePointer] ← NewItem //将数据存入尾指针指向的数据单元
　　　　NumberInQueue ← NumberInQueue + 1 //队列内的数据个数加1
　　ENDIF
ENDPROCEDURE

• • 从队列中删除一个数据：

FUNCTION RemoveFromQueue() //无需参数输入，但会返回需要弹出的数据
　　DECLARE Item: STRING //定义一个变量来记录删除的数据
　　Item ← EMPTYSTRING //初始化变量为空字符串
　　IF NumberInQueue > 0 //如果队列中有数据（不为空）
　　　THEN
　　　　Item ← Queue[FrontOfQueuePointer] //要删除的数据为队列首指针指向的数据（先进先出）
　　　　NumberInQueue ← NumberInQueue – 1 //队列中的数据个数减1
　　　　IF NumberInQueue = 0 //如果移除数据后队列中没有其他数据（删除了唯一一个数据后）}}
　　　　　THEN
　　　　　　CALL InitialiseQueue //初始化队列（重新整理首尾指针）
　　　　 ELSE //如果移除数据后队列中仍有其他数据
　　　　　　FrontOfQueuePointer ← FrontOfQueuePointer + 1 //首指针下移1位，代表上一位的数据单元已经不在队列中
　　　　　　IF FrontOfQueuePointer > MaxQueueSize – 1 //如果当前首指针超过了队列数组的最大位置，则考虑循环队列（如果没超则跳过此处的代码，按照正常情况以下移后的数据单元作为队列的首项即可）
　　　　　　　THEN
　　　　　　 FrontOfQueuePointer ← 0 //将首指针指向数据首项，形成循环队列
　　　　　　ENDIF
　　　　ENDIF
　　ENDIF
　　RETURN Item //返回要删除的数据值
ENDFUNCTION

• 关于graph图：【参考18.1.1】

19.1.4 Show how it is possible for ADTs to be implemented from another ADT 展示如何从另一个 ADT 实现 ADT

Describe the following ADTs and demonstrate how they can be implemented from appropriate built-in types or other ADTs: stack, queue, linked list, dictionary, binary tree 描述以下 ADT 并演示如何从适当的内置类型或其他 ADT 中实现它们：堆栈、队列、链表、字典、二叉树

• 栈、队列、链表和二叉树的部分【参考19.1.3】。
• Hash table：哈希表。使用哈希表是为了能够直接访问存储在数组中的记录位置。通过记录key值的计算获取地址，然后将记录存入数组。当需要访问该记录时，通过key值计算出存放地址，则可以直接访问。
  • Collision：冲突，指通过key值的计算，获得的数组存储地址是同一个。解决冲突的常见做法如下：
    • 方法一：将冲突的数据都记入一个新链表，然后将hash table哈希表中的位置改为记录链表的地址。
    • 方法二：closed hashing封闭散列。将所有冲突都记入一个独立的overflow area溢出区。
    • 方法三：open hashing开放散列。遇到冲突时，在冲突位置后使用线性搜索找到一个空位置，将数值存入该空位置。
  • 处理哈希表中的存储与冲突的例子：将45876、32390、95312、64636、23467这几个数字存入哈希表内。
    • 计算key值的函数为：Index ← CustomerID MOD 10
    • 前三个值计算后分别是6、0、2，不存在冲突，直接计入数组中的相应位置。如下图所示：

• • • 第四个值计算后为6，而此时编号为6的数组中已经有数值了，因此发生冲突。可采取顺延的方式，在其后找一处空位置，将第四个值存入。因为编号为7的数组是空的，因此将第四个值64636存入该位置。如下图所示：

• • • 第五个值计算后为7，而此时编号为7的数组中已经有数值了，因此发生冲突。可采取顺延的方式，在其后找一处空位置，将第五个值存入。因为编号为8的数组是空的，因此将第五个值23467存入该位置。如下图所示：

• • 向哈希表中插入一个新数据：

PROCEDURE Insert(NewRecord)
　　Index ← Hash(NewRecord.Key) //根据函数关系算出应存储的数组位置
　　WHILE HashTable[Index] NOT empty DO //如果该位置不为空（已经存在数据，冲突发生）
　　　　Index ← Index + 1 //向后顺延一位，等待再次进入循环条件确认
　　　　IF Index > Max //如果顺延后的位置超出了数组边界，需要考虑循环数组
　　　　 THEN
　　　　　　Index ← 0 //将存储位置指向数组首位（首尾相接）
　　　　ENDIF
　　ENDWHILE
　　HashTable[Index] ← NewRecord //将新数据存入哈希表内
ENDPROCEDURE

• • 从哈希表中查找一个数据的位置：

FUNCTION FindRecord(SearchKey) RETURNS Record //输入搜索数据的key值，返回查询到的记录
　　Index ← Hash(SearchKey) //根据提供的key值，计算出存储的数组位置
　　WHILE (HashTable[Index].Key <> SearchKey) //如果根据计算找到的存储位置中的值与搜索值不同（即有冲突情况发生。注意，如果此时数值相同，表示找到了相应的数据，会直接跳出循环，Index值即为存储该数据的数组位置）
　AND (HashTable[Index] NOT empty) DO //并且哈希表存在数值（不为空），则进入循环
　　　　Index ← Index + 1 //向后顺延一位，等待再次进入循环条件确认
　　　　IF Index > Max //如果顺延后的位置超出了数组边界，需要考虑循环数组
　　　　　THEN
　　　　　　Index ← 0 //将存储位置指向数组首位（首尾相接）
　　　　ENDIF
　　ENDWHILE
　　IF HashTable[Index] NOT empty //如果数值找到了
　　　THEN
　　　　RETURN HashTable[Index] //返回找到的记录
　　ENDIF ENDFUNCTION

• Dictionary：字典，指Key值和数值的对应关系。计算机中的字典是通过hash table哈希表来实现的，因此可以通过输入key值后直接访问需要的数值。
  • 创建一个字典：

TYPE DictionaryEntry //定义一个记录类型，保存对应的key值和数值
　　DECLARE Key: STRING
　　DECLARE Value: STRING
ENDTYPE
DECLARE EnglishFrench: ARRAY[0 : 999] OF DictionaryEntry //定义一个记录类型的数组，形成一个字典（默认是空字典）

19.1.5 Show understanding that different algorithms which perform the same task can be compared by using criteria (e.g. time taken to complete the task and memory used) 理解执行相同任务的不同算法可以通过使用标准进行比较（例如完成任务所用的时间和使用的内存）

Including use of Big O notation to specify time and space complexity 包括使用大 O 表示法来指定时间和空间复杂度

• Big O notation：大O表示法，指根据算法的运行时间（或空间需求）如何随输入数据规模增长而增长来对算法效率进行估计的方法。函数的运行时间（或空间需求）增长速度也被称为order of the function函数阶数。阶数越高，算法的效率越差。
  • Best-case scenario：最优情况，即当数据完全符合要求，无需调整时，算法运行一次需要的阶数。
  • Worst-case scenario：最差情况，即当数据全部需要调整时，算法运行一次需要的阶数。当输入数据的规模很大时，要按照最差情况去考虑。

• Time complexity：时间复杂度，指算法耗费的时间增长情况。通过关注循环内核心语句的循环方式，取最大的时间耗费情况。
  • 常见的算法时间复杂度：

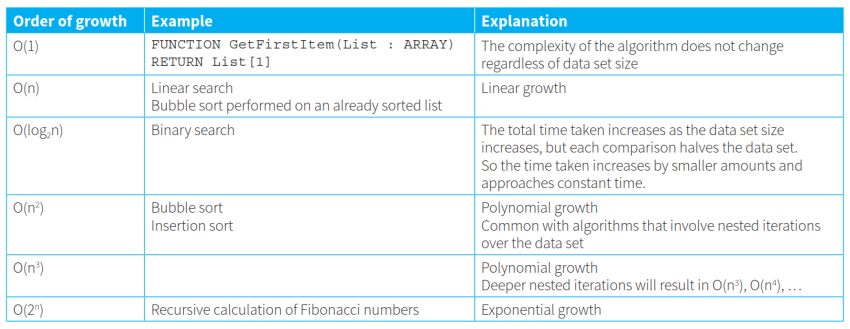
• Space complexity：空间复杂度，指算法耗费的内存空间增长情况。

19.2 Recursion 递归

• 大纲要求

19.2.1 Show understanding of recursion 展示对递归的理解

Essential features of recursion. 递归的基本特征。
How recursion is expressed in a programming language. 递归在编程语言中是如何表达的。
Write and trace recursive algorithms 编写和跟踪递归算法
When the use of recursion is beneficial 当使用递归是有益的时候

• Recursion：递归。如果一个函数或过程是根据自身来定义的（类似于“套娃”），则称之为递归。
  • 递归过程的必要条件与结构分析：递归过程由base case基本情况与general case一般情况构成。
    • base case：基本情况，指不涉及一般情况（即自身定义）的情况，是递归的终结条件。
    • general case：一般情况，指根据定义本身进行定义的情况，是定义“套娃”的部分，但每次递归时，一般情况的变化必须更加靠近基本情况，直到递归到基本情况为止。
• 递归程序的编写：
  • 注意：递归程序必须满足有基本情况、有一般情况、一般情况在通过有限次的调用后能达到基本情况。否则，程序会出错（比如陷入死循环、内存溢出等）
  • 运用函数进行递归运算的例子：计算n的阶乘。

FUNCTION Factorial(n: INTEGER) RETURNS INTEGER //输入数值n，输出目前为止计算出的阶乘值
　　IF n = 0
　　　THEN
　　　　Result ← 1 {{{2}}}
　　 ELSE
　　　　Result ← n * Factorial(n – 1) //一般情况，反复调用自身以完成递归运算
　　ENDIF
　　RETURN Result //将目前为止计算出的阶乘值输出
ENDFUNCTION

• • 运用过程进行递归运算的例子：将数字倒序输出。

PROCEDURE CountDownFrom(n: INTEGER) //输入数值n
　　OUTPUT n {{{2}}}
　　IF n > 0
　　　THEN
　　　　CALL CountDownFrom(n – 1) //一般情况，反复调用自身以完成递归
　　ENDIF
ENDPROCEDURE

• 递归程序的tracing追踪：可使用trace table追踪表来对递归程序每一步的输出和判断进行追踪。
  • 使用trace table追踪表追踪递归过程的例子：对数据进行从0到n的正序输出。
    • 代码：

PROCEDURE CountUpTo(n: INTEGER) //输入数值n，输出目前为止计算出的阶乘值
　　IF n > 0
　　　THEN
　　　　CALL CountUpTo(n – 1) //一般情况，反复调用自身以完成递归
　　ENDIF
　　OUTPUT n {{{2}}}
ENDPROCEDURE

• • • 追踪表：

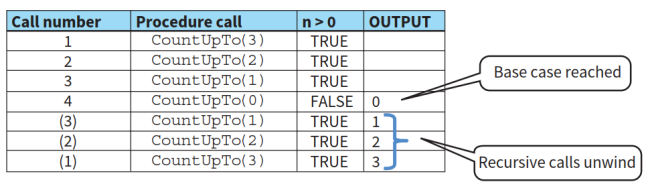
• • • • 说明：由于递归程序需要调用自身，因此在调用完成之前，后续语句均不会执行。因此前三步没有直接的输出。第4步调用时进入基本情况，输出0。该层递归关闭，返回上一层递归，继续执行后续语句，输出值1。后续操作以此类推，直到全部递归程序关闭。
  • 使用trace table追踪表追踪递归函数的例子：计算n的阶乘值。
    • 代码：

FUNCTION Factorial(n: INTEGER) RETURNS INTEGER //输入数值n，输出目前为止计算出的阶乘值
　　IF n = 0
　　　THEN
　　　　Result ← 1 //基本情况，递归到n=0时将会结束递归
　　 ELSE
　　　　Result ← n * Factorial(n – 1) //一般情况，反复调用自身以完成递归运算
　　ENDIF
　　RETURN Result //将目前为止计算出的阶乘值输出
ENDFUNCTION

• • • 追踪表：

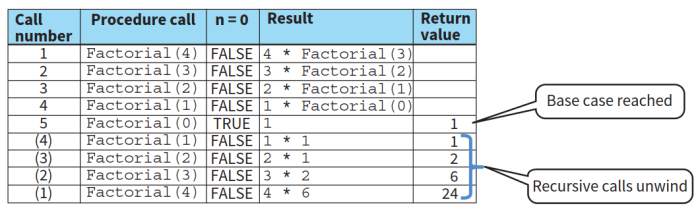
• • • • 说明：因为函数每一步都有返回中途的结果，因此加了一列result。
      • 说明：由于递归程序需要调用自身，因此在调用完成之前，后续语句均不会执行。因此前四步没有直接的输出。第5步调用时进入基本情况，输出1。该层递归关闭，返回上一层递归，将之前计算的数值1带入本层的计算，执行后续语句，输出值1。后续操作以此类推，直到全部递归程序关闭。
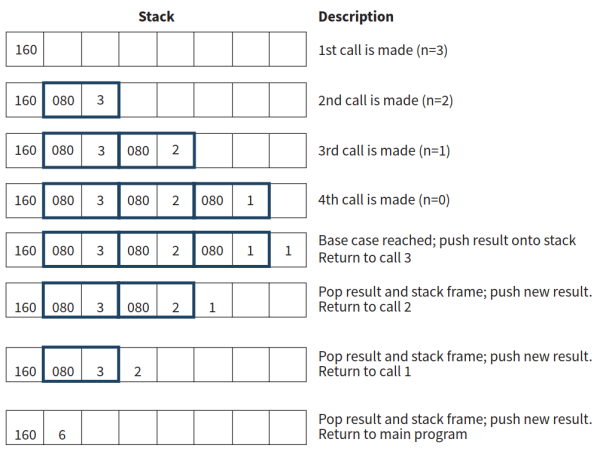
  • 有时候递归也可以采用box的形式展现，递归一路进入最内部的盒子（即基本情况），然后逐步返回，直至全部递归程序运行完毕。如下图所示：

• 使用递归的好处：
  • 思路简单易懂。
  • 代码简洁。
• 使用递归的问题：
  • 占用大量内存与时间（时间复杂度为指数级，空间上需要大量栈来完成递归）。

19.2.2 Show awareness of what a compiler has to do to translate recursive programming code 了解编译器必须做什么来翻译递归编程代码

Use of stacks and unwinding 使用堆垛和放卷

• 编译器运行递归的操作：编译器在运行递归操作时，使用的object code目标代码是将递归部分的参数和运行地址不断压入栈中。如果遇到了基本情况，则不断将已经运算完毕的部分弹出栈参与运算（回溯）。如下图所示：