CAIE AS and A Level CS revision - Unit 1 (2nd)

【点此返回复习要点目录】

如遇到公式加载异常，请刷新页面！

Unit 1 Information representation 信息表示（AS）

1.1 Data Representation 数据表示

• 大纲要求

1.1.1 Show understanding of binary magnitudes and the difference between binary prefixes and decimal prefixes 了解二进制大小以及二进制前缀和十进制前缀之间的区别

Understand the difference between and use: 了解区别并学会使用：
· kibi and kilo
· mebi and mega
· gibi and giga
· tebi and tera

• Denary numbers：十进制数字，逢十进一。
  • 每个数位上的数字可能是0~9中的一个，如318。
  • 每个数位代表10的次方数，如318=3×10²+1×10¹+8×10⁰
• Binary numbers：二进制数字，逢二进一。
  • Bit：比特，每个二进制数位上的数字即为1比特。
  • 每个数位上的数字可能是0~1中的一个，如1011。
  • 如果使用带符号的二进制码，则首位代表符号，0为正号，1为负号。
  • Byte：字节。1 byte = 8 bit。
• Hexadecimal numbers：十六进制数字，逢十六进一。
  • 每个数位上的数字可能是0~9、A~F中的一个，如2A6。

• Decimal prefixes：十进制前缀，如kilo、mega、giga和tera。这些前缀代表的数字是以10为底的指数级。具体大小如下图所示。

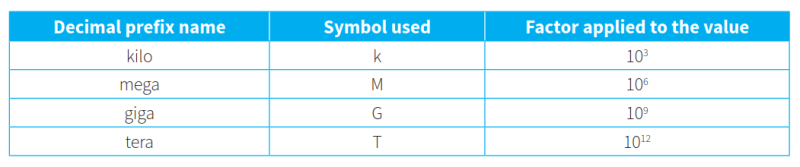
• Binary prefixes：二进制前缀，如kibi、mebi、gibi和tebi。这些前缀代表的数字是以2为底的指数级。具体大小如下图所示。

• • 1 KiB=2¹⁰ bytes，后续单位的转换均是2¹⁰。
  • 现在计算机相关领域更多地使用Binary prefixes来进行表达，更加精确。但生活中很多时候为方便表述，有时也会使用decimal prefixes描述。

1.1.2 Show understanding of the basis of different number systems 了解不同数字系统的基础

Use the binary, denary, hexadecimal number bases and Binary Coded Decimal (BCD) and one’s and two’s complement representation for binary numbers 使用二进制、十进制、十六进制和二进制编码十进制 (BCD) 以及二进制数的反码和补码的表示
Convert an integer value from one number base / representation to another 将整数值从一个进制转换为另一个进制

• Binary Coded Decimal (BCD)：用4位的二进制码（0000~1001）表示十进制数字0~9。
  • 比如十进制数8503可用下列BCD表示（每个数字使用1个byte）：

• • Packed BCD：每个数位采用四位二进制码表示，一个字节（八位二进制码）就可以表示两个数位。这是因为十进制下的0~9只需要四位二进制码0000~1001就可以完全表示，两个数位正好拼成一个字节。比如十进制数8503可用下列packed BCD表示：

• • 采用BCD进行十进制数字的加法运算时，每个十进制数位（采用packed BCD时）加减完毕后，如果大于1001（大于十进制下的9），需要加上二进制数字0110进行进位修正。这是因为二进制数字的低四位向高数位是十六进一，而十进制数字是十进一，所以需要通过加0110（加6）来使得二者进位规则相同。

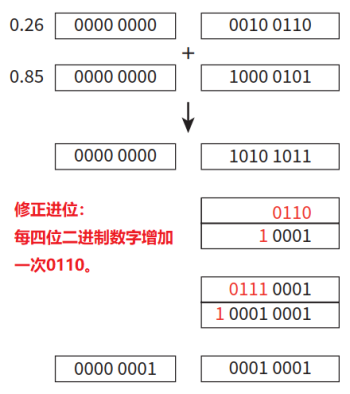
• One’s complement：反码。二进制数字每一位做如下变化：原来的1变为0，原来的0变为1。如1010变为0101。
• Two’s complement：补码。二进制数字的one’s complement反码加1。
  • 便捷求two’s complement补码的方法：从右往左寻找第一个不为0的数位，忽略掉该数位和右侧的0，该数位前面的部分（不包含该数位），原来的1变为0，原来的0变为1，然后和忽略掉的部分连接。
    • 比如：10100100的补码寻找过程：从右往左，忽略掉尾部的100，前面10100这一部分全部翻转，成为01011，然后和忽略掉的部分连接，得到01011100，即为其补码。
    • 使用补码可以把减法运算变成加法运算，以此来简化逻辑算术单元设计。（负数以补码形式表示，可简化计算）
      • 十进制中的正数的补码为其本身的二进制数字。
      • 十进制中的负数补码的求法过程为：忽略负号，将其绝对值转换成二进制数字，在二进制首位加一个0表示正数，然后对该数求补码。（该过程可逆）
        • 比如：-1忽略负号，得到二进制码0001，然后求补码得到1111，即为-1的补码。
      • 补码的补码为原码。（恢复回原来的数字）
      • 代表负数的二进制原码求补码，将首位的1改为0后，求其补码。
        • 比如：二进制码1001表示-1，将首位的1改为0得到0001，然后求补码得到1111，即为-1的补码。

• 二进制转十进制：每个二进制数位乘上相应的以2为底的次方数（由右向左分别为2的0、1、2次方等），然后相加。
  • 比如：1011=1×2³+0×2²+1×2¹+1×2⁰=11。
• 十六进制转十进制：每个十六进制数位乘上相应的以16为底的次方数（由右向左分别为16的0、1、2次方等），然后相加。注意，A~F分别代表十进制中的10~15。
  • 比如：2A6=2×16²+10×16¹+6×16⁰=678。

• 十进制转二进制：用十进制数字不断除2，直到商为0停止，每次取得的余数倒置排列，排列出的数字即为转换后的二进制数字。
  • 比如：十进制数字246转换后的二进制数字为11110110，过程如下图所示。

• 十进制转十六进制：
  • 方法1：用十进制数字不断除16，直到商为0停止，每次取得的余数倒置排列，排列出的数字即为转换后的十六进制数字。余数为10~15时，使用A~F表示。
  • 方法2：将十六进制数字先转换为二进制数字，然后再由二进制数字转换为十进制数字。

• 二进制转十六进制：
  • 由右向左起，每四位二进制数字写成一个十六进制数字。当二进制数字不足四位时用0补足数位，然后将转换好的数字从左到右连接起来。
    • 比如：二进制数字11000101转为十六进制时，1100转为C，0101转为5，所以该二进制数字转为十六进制数字C5。
• 十六进制转二进制：
  • 十六进制数字的每个数位都用四位的二进制数字表示，不足四位时用0补齐数位，然后将转换好的数字从左到右连接起来。
    • 比如十六进制数字B4转为二进制时，B转为1011，4转为0100，所以该十六进制数字转为二进制数字10110100。

1.1.3 Perform binary addition and subtraction 执行二进制加减法

Using positive and negative binary integers 使用正负二进制整数
Show understanding of how overflow can occur 了解溢出是如何发生的

• 通常一个二进制数是n位时，能够表示0~(2n-1)之间的数字。但如果选择使用signed and magnitude representation带符号的大小表示，则首位用于表示符号，正号为0，符号为1，剩下位数表示数字，该类型能够表示-2n-1~(2 n-1-1)之间的数字。
  • 比如：如果采用无符号表达，1110代表14。如果采用有符号表达，则首位的1代表符号，后面的110代表数字6，则1110代表的实际数字是-6。

• 二进制加法：逢二进一。
  • 比如1011 + 1110 = 11001（注意是否溢出）

• 二进制减法：二进制减法统一采用补码加法计算，即将减法看成是加上一个负数，将减数视为负数取其Two’s complement补码，然后加到被减数上。
  • 注意：需要查看是否存在溢出的情况。如果结果存在溢出，则需要以非符号位加0的方式扩展二进制位数，直到不再发生溢出现象为止。
  • 注意：结果的位数与参与计算的数值位数一致。当结果计算完毕后，超过位数的部分将被舍弃（删除不看）。
  • 注意：参与计算的数值位数应当保持一致，如果位数不一致，以最多位数为准，位数少的在非符号位加0补齐位数。
  • 比如：67-35的计算可按照如下步骤进行：
    • 将减法看成是加上负数的计算，67+(-35)。
    • 计算将67和-35转换为二进制，得到01000011（对应67）和1100011（对应-35）。
    • 检查数位情况，-35对应的二进制码短，补齐为10100011。
    • 检查溢出情况。67和-35的二进制码最高位相加进位为0，第二位相加进位为0，因此不存在溢出的现象。
    • 对-35的二进制码求Two’s complement补码，其补码为11011101。【参考1.1.2】67的二进制补码为其本身。
    • 将二者的补码相加，得到(1)00100000。括号中的1超出了参与计算数据的最高数位8位，该部分将被自然舍弃。因此67-35的结果的二进制码为00100000，即对应十进制的32，结果正确。

• Overflow：溢出，即计算的数位超出应有的数位而导致的结果，会使得计算结果出现偏差。（尤其是符号出现错误）。
  • 判断溢出的方法：可采用双符号法，将数字的二进制码位数补齐后，计算其最高位相加的进位值和次高位相加的进位值，如果二者相同（都是0或都是1），则没有溢出现象；如果二者不同（一个是1一个是0），则出现溢出现象，01型是正溢出（超过能表示的最高值），10型是负溢出（低于能表示的最低值）。

1.1.4 Describe practical applications where Binary Coded Decimal (BCD) and Hexadecimal are used 描述使用二进制编码十进制 (BCD) 和十六进制的实际应用

• BCD的应用实例：计算器、电子钟等需要展示固定位数的情况。（如果以real类型展示可能不准确）
• Hexadecimal十六进制的应用：由于一个2个十六进制位数就是一个字节，因此在计算机中广泛使用。

1.1.5 Show understanding of and be able to represent character data in its internal binary form, depending on the character set used 理解并能够以内部二进制形式表示字符数据，具体取决于所使用的字符集

Students are expected to be familiar with ASCII (American Standard Code for Information Interchange), extended ASCII and Unicode. Students will not be expected to memorise any particular character codes 学生应熟悉 ASCII（美国信息交换标准代码）、扩展 ASCII 和 Unicode。学生不会被要求记住任何特定的字符代码

• ASCII code：美国信息交换标准码，以7位二进制码表示，共128个。平时为了方便记忆，会使用十进制数字表达。第48-57个code为0~9，第65-90个code为大写字母A-Z，第97-122个code为小写字母a-z。
• Extended ASCII：扩展的ASCII码，以8为二进制码表示。
• Unicode：统一码，通过特殊的编码形式，将世界上几乎所有字符与符号编入其中。最常见的是UTF-8。
  • UTF-8的编码形式：可采用1字节、2字节、3字节或4字节方式编码（国际标准要求）。其中第一个字节中1的数量表示一共用到了多少个字节，后续每个字节均以10开头。
    • 采用1字节（前0~127号）时，二进制码和ASCII相同。
    • 采用2字节（前128~2047号）时，第1字节开端占用110，第2字节开端占用10，剩余11个空位可用于编写字符代码。
    • 采用3字节（前2048~65535号）时，第1字节开端占用1110，第2、3字节开端占用10，剩余16个空位可用于编写字符代码。
    • 采用4字节（前65536~2097151号）时，第1字节开端占用11110，第2、3、4字节开端占用10，剩余21个空位可用于编写字符代码。

1.2 Multimedia 多媒体

• 大纲要求

1.2.1 Graphics 图形

1.2.1.1 Show understanding of how data for a bitmapped image are encoded 了解如何对位图图像的数据进行编码

Use and understand the terms: pixel, file header, image resolution, screen resolution, colour depth, bit depth 使用和理解术语：像素、文件头、图像分辨率、屏幕分辨率、颜色深度、位深度

• Bitmap：位图，指由像素点组成的图像。
  • Pixel：像素。位图的最小组成元素，类似数学中“点”的概念。位图被看成是以二维的像素点组成的图像。像素带有颜色。
  • File header：文件头。在其中包含着对位图的colour depth、bit depth、image resolution等相关的编码信息，以用于读取、显示和保存位图。
  • Image resolution：图像分辨率。指图像的长、宽分别包含多少像素。
  • Screen resolution：屏幕分辨率。指屏幕的长、宽能够显示多少像素。
  • Bit depth：位深。指RGB颜色编码中，储存红、绿、蓝三原色编码的数位。如果每个原色采用8位编码，则一共能提供256种原色方案，三原色一共能创造出2563=16777216种颜色。
  • Colour depth：色深。指每个像素中包含的二进制数位。数位越多，其色深就越大。
    • Colour depth = 3 * bit depth（因为一共是红、绿、蓝三种颜色）

1.2.1.2 Perform calculations to estimate the file size for a bitmap image 执行计算以估计位图图像的文件大小

• 位图图像的位数bit = Image resolution × Colour depth
  • 比如：Colour depth为24，Image resolution为1366×768，则位图大小为1366×768×24=25178112 bits。
• 位数计算完成后，将其用合适的binary prefixes表达。
  • 比如：25178112 bits = 3147264 bypes = 3073.5 kibi = 3MiB

1.2.1.3 Show understanding of the effects of changing elements of a bitmap image on the image quality and file size 了解更改位图图像元素对图像质量和文件大小的影响

Use the terms: image resolution, colour depth/bit depth 使用术语：图像分辨率、颜色深度/位深度

• 位图如果未进行分辨率的修改调整，仅改变大小并不会改变像素数量的多少。在拉伸过程中，如果达到了人眼的识别率，像素块就会被看到，从而出现“虚化”的现象，图像质量下降。
• 如果想合理放大位图，可拉伸到人眼暂不能识别像素块的大小，或者调高分辨率以清晰显示。如果调高了分辨率，则位图大小会随之增加。

1.2.1.4 Show understanding of how data for a vector graphic are encoded 了解矢量图形数据的编码方式

Use the terms: drawing object, property, drawing list 使用术语：绘图对象、属性、绘图列表

• Vector graphic：矢量图形，由各类绘制对象组成的图形。
  • drawing object：图形对象，是组成矢量图形的最小单位。
  • property：属性，指的是drawing object图形对象的某个特征。一个对象可能有很多个property属性。
  • drawing list：图形目录，指包含了图像中全部图形对象的列表。
• 矢量图是通过一系列的属性来表达图形，比如给定圆心和半径来绘制图形，因此只需改变计算参数即可绘制出新的图形，可以随意放大缩小而不会影响其清晰度。
  • 矢量图的显示只能在专用机器上实现，在无法显示矢量图的机器上使用时需要先转换成bitmap位图。

1.2.1.5 Justify the use of a bitmap image or a vector graphic for a given task 证明对给定任务使用位图图像或矢量图形的合理性

• 在architectural, engineering or manufacturing design建筑、机械和制造设计方面，使用vector graphic矢量图形。
• 如果需要使用激光或喷墨打印图像，则需要使用或转换成bitmap位图。
• 数码相机直接生成bitmap位图。
• 文档中插入图片、出版物编辑、网页制作等使用的都是bitmap位图。

1.2.2 Sound 声音

1.2.2.1 Show understanding of how sound is represented and encoded 了解声音是如何表示和编码的

Use the terms: sampling, sampling rate, sampling resolution, analogue and digital data 使用术语：采样、采样率、采样分辨率、模拟和数字数据

• Sound：声音。计算机需要通过一系列编码，将声波转化为二进制码进行处理和保存。
  • Sampling：采样。按照一定时间间隔对初始的模拟信号进行样本采集并保存，以进行下一步处理。
  • sampling rate：采样率，指每秒采样的数量，即采样速度。
    • 按照Nyquist’s theorem，采样率必须至少保持为样本音频最高频率的2倍。
  • sampling resolution：采样分辨率，指用于储存每次采样而使用的二进制码位数。
  • analogue and digital data：
    • analogue data：模拟数据，指采用物理手段获得的连续声音数据。
    • digital data：数字数据，指采用二进制码记录数值获得的声音数据。

1.2.2.2 Show understanding of the impact of changing the sampling rate and resolution 了解改变采样率和分辨率的影响

Including the impact on file size and accuracy 包括对文件大小和准确性的影响

• 音频大小（bits）= sampling rate * sampling resolution * 声道数 * 时间（秒），得到数值后再换算成合适的单位（如KiB、MiB等）。
• Analogue data模拟数据需要通过转换为digital data数字数据进行保存。在转换过程中，sampling rate取样率越高，resolution分辨率越高，保存下来的数字数据就越接近原来的模拟数据（accuracy精确度越高），但file size文件大小也越大。

1.3 Compression 压缩

• 大纲要求

1.3.1 Show understanding of the need for and examples of the use of compression 展示对压缩的需要和使用示例的理解

• 大文件的传输、下载速度较慢，影响了数据传播的速度，因此需要进行压缩。

1.3.2 Show understanding of lossy and lossless compression and justify the use of a method in a given situation 展示对有损和无损压缩的理解，并证明在给定情况下使用方法的合理性

• lossless compression：无损压缩，指文件大小减少但信息没有缺失，随时可以还原成之前没有压缩的文件。
  • 注意：如果文件中包含text文本，则必须是无损压缩。
• lossy compression：有损压缩，指文件大小减少，信息有所缺失，无法再次还原成之前没有压缩的文件。

1.3.3 Show understanding of how a text file, bitmap image, vector graphic and sound file can be compressed 了解如何压缩文本文件、位图图像、矢量图形和声音文件

Including the use of run-length encoding (RLE) 包括使用游程编码（RLE）

• run-length encoding (RLE)：游程编码，指将重复的编码以“数量×重复部分”的形式进行压缩以减小文件大小。该压缩属于无损压缩。
  • 比如重复出现的01100110被写成“4个01100110”，如下图所示。

• Huffman coding：霍夫曼编码，指通过最优二叉树的排序为内容赋code值，解码时按照二叉树的路线结构返回原样。
  • 霍夫曼编码可用于sound file声音文件。
  • 具体编码步骤如下：将不同类别内容的出现频次进行统计，由低到高排序。将最低频次的类别作为左子树，次低频次的作为右子树，根为二者频次之和。将根的数值参与和其他类别频次的排序，按照上述步骤反复进行，直到所有类别全部排入二叉树。将所有左子树路径设定为0，右子树路径设定为1，按照从根到叶的顺序为每一个类别确定其二进制码表示。如下图所示。

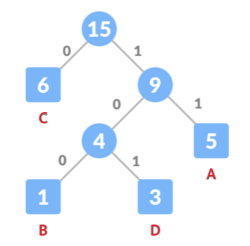
类别	二进制码
A	11
B	100
C	0
D	101

• Vector graphic矢量图形如果需要压缩，可转换为Scalable Vector Graphics文件类型。该形式属于无损压缩。
• Sound file声音文件和bitmap位图可以进行有损压缩，只要在人耳或人眼无法识别出区别的范围内进行压缩即可，因此一些细节部分可以被省略。
  • Sound file声音文件可考虑降低取样分辨率，或将time domain data时域数据转为frequency domain data频域数据（频域数据需要的储存空间更小）。
  • Bitmap位图可考虑降低colour depth色深。